The demand for action figures based on characters from children's movies is extremely high around the time the movie is released. In this peak period, demand for action figures is 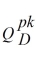
= 300,000 - 10,000P P = 30 - 0.0002 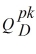
.
The resulting marginal revenue curve is MR(Qpk) = 30 - 0.0004 Qpk. Some time after the movie release, interest in the action figures wanes. In this lull period, demand for the action figures becomes 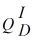
= 100,000 - 25,000P P = 4 - 0.00008 
. The resulting lull period marginal revenue curve is MR(QI) = 4 - 0.00016 QI. Suppose the marginal costs of producing the action figures are constant at $1.50. What is the optimal pricing strategy in the two different periods?
Definitions:
Profits and Losses
Financial gains when revenues exceed expenses or financial losses when expenses surpass revenues, respectively.
Interest Rate
The percentage of a sum of money charged for its use, typically expressed as an annual percentage rate.
Future Value
The value of a current asset at a future date based on an assumed rate of growth over time.
Free-Land Era
A historical period characterized by the availability and acquisition of land for free or at minimal cost, often associated with westward expansion in the United States.
Q8: In less-competitive domestic M&A markets, winners often
Q14: A global bond is an international bond
Q23: Suppose a competitive industry produces output, Q,
Q41: Refer to Scenario 13.1. If your negotiated
Q42: The two largest auto manufacturers, Toyota and
Q47: _ questions have to do with explanation
Q52: Which of the following goods is NOT
Q76: Refer to Scenario 10.3. Suppose that a
Q78: Which is true of output-choice models of
Q91: The authors explain that the marginal cost