Vector 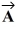
has a magnitude of 5.5 cm and points along the x-axis. Vector 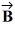
has a magnitude of 7.5 cm and points at +30° above the negative x-axis.
(a) Determine the x and y components of Vector 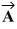
.
(b) Determine the x and y components of Vector 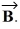
(c) Determine x and y components of the sum of these two vectors.
(d) Determine the magnitude and direction of the sum of these two vectors.
Definitions:
Arthur
In the context of economics, Arthur does not directly relate to a specific key term; in other contexts, it could refer to a person's name or a historical figure.
Nash Equilibrium
A concept in game theory where no player can benefit by changing strategies while the other players keep theirs unchanged, indicating optimal decision-making among competitors.
Michigan Football
The football team representing the University of Michigan, known for its history and achievements in college football.
Gain Yards
A term often used in American football to describe the act of advancing the ball closer to the opposing team's goal line.
Q11: A microwave oven operates with sinusoidal microwaves
Q13: In the figure, the magnitude of vector
Q13: In the figure, a bar magnet moves
Q15: Electric charge is uniformly distributed inside a
Q17: If the accuracy in measuring the velocity
Q27: It is desired to project the image
Q32: A series LRC circuit consists of a
Q36: Suppose that in a parallel universe, the
Q37: A non-conducting sphere of radius R =
Q65: The figure shows three metal coils labeled