Consider the Following Scenario to Answer the Questions That Follow

question 92

Multiple Choice

Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
-Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant will receive the gold bar that is under his or her bucket. The host of the game show asks the contestant to choose one of the three buckets.The contestant chooses bucket #1.After the contestant makes a choice,the host lifts up bucket #2 to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose (bucket #1) and the bucket that was not uncovered by the host (bucket #3) .
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.The contestant changes buckets from the original bucket (bucket #1) to the other bucket remaining (bucket #3) .When the contestant originally made the choice of bucket #1,the probability of the 5-oz.gold bar being under that bucket was 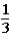.This means that the probability of the 5-oz.gold bar being under either bucket #1 or bucket #2 was 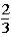.When the host lifted bucket #2 to reveal a 1-oz.gold bar under it,the probability of the 5-oz.gold bar being under bucket #3 is now ____________,while the probability of the 5-oz.gold bar being under bucket number #1 is still _____________.

• A) ;
• B) ;
• C) ;
• D) ;
• E) ;

---

Definitions:

Assembly Kits

Pre-packaged sets of parts or components intended to be assembled by the consumer into a complete product.

Luxury Items

Goods or services that are considered indulgent or non-essential, characterized by high quality, price, and status symbol.

Radio Airwaves

Electromagnetic waves used for transmitting sound messages through devices like radios; crucial for broadcasting.

Immorality

Behavior that violates moral or ethical principles, often socially defined and varying greatly across different cultures and communities.