Use the Case Below to Answer the Following Question(s)

question 42

Multiple Choice

Use the case below to answer the following question(s) .
The Tipton Hotel is considering a major remodeling effort and needs to determine the best combination of rates and suite sizes to maximize revenues.Currently,the hotel has 755 suites with the following history: 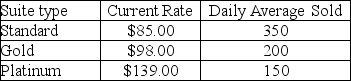Each market segment has its own price/demand elasticity.Estimates are: 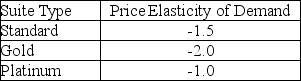This means,for example,that a 1% decrease in the price of a standard suite will increase the number of suites sold by 1.5%.Similarly,a 1% increase in the price will decrease the number of suites sold by 1.5%.For any pricing structure (in $) ,the projected number of suites of a given type sold (we will allow continuous values for this problem) can be found using the formula:
(Historical average number of suites sold) + (Elasticity) (New price - Current price) (Historical average number of suites sold) /(Current price)
The hotel owners want to keep the price of a standard suite between $70 and $90; a gold suite between $90 and $110; and a platinum suite between $120 and $149.
Define S = price of a standard suite,G = price of a gold suite,and P = price of a platinum suite.
-Determine the projected revenue for selling the projected number of platinum suites.

• A)$20,938.78
• B)$20,762.98
• C)$30,491.55
• D)$72,193.31

---

Definitions:

Standard Normal

A typical distribution that has a mean value of 0 and a standard deviation value of 1.

Obtaining

The act of gaining possession of something, usually after an effort.

Uniformly Distributed

A distribution where all outcomes are equally likely, and the variable's values are spread evenly over the range of possibilities.

Probability Density Function

A probability density function is a function that describes the probability of a random variable taking on certain values, used for continuous variables where the probability of any single value is zero.