Examlex

Solved

TABLE 15-4 the Superintendent of a School District Wanted to Predict the Predict

question 20

Multiple Choice

TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination ( TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the best model chosen using the adjusted R-square statistic is A) X<sub>1</sub>,X<sub>3</sub>. B) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. C) Either of the above D) None of the above ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
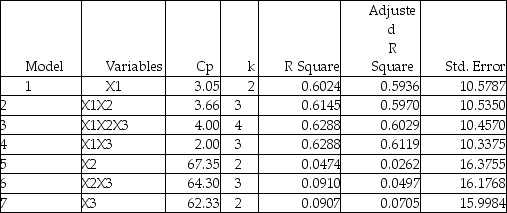The output from the best-subset regressions is given below: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the best model chosen using the adjusted R-square statistic is A) X<sub>1</sub>,X<sub>3</sub>. B) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. 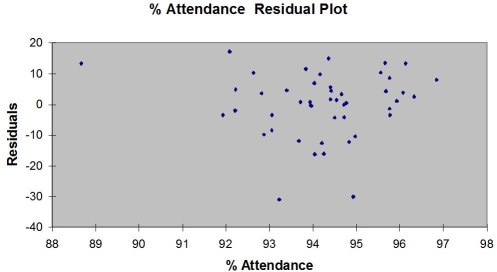C) Either of the above D) None of the above Following is the residual plot for % Attendance: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the best model chosen using the adjusted R-square statistic is A) X<sub>1</sub>,X<sub>3</sub>. B) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. C) Either of the above D) None of the above Following is the output of several multiple regression models:
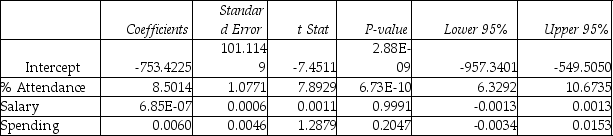Model (I) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the best model chosen using the adjusted R-square statistic is A) X<sub>1</sub>,X<sub>3</sub>. B) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. 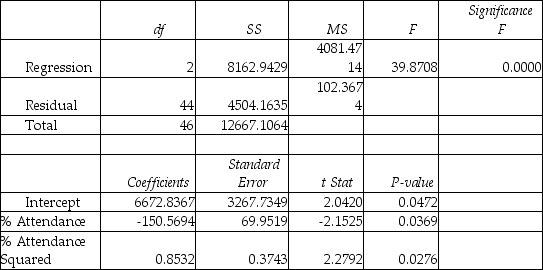C) Either of the above D) None of the above Model (II) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the best model chosen using the adjusted R-square statistic is A) X<sub>1</sub>,X<sub>3</sub>. B) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. C) Either of the above D) None of the above Model (III) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the best model chosen using the adjusted R-square statistic is A) X<sub>1</sub>,X<sub>3</sub>. B) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. C) Either of the above D) None of the above
-Referring to Table 15-4,the "best" model chosen using the adjusted R-square statistic is

Definitions:

Low Self-Esteem

A condition characterized by a lack of confidence in one's own worth or abilities.

Unrealistic Optimism

The tendency to overestimate the probability of positive outcomes and underestimate the likelihood of negative events.

Technophobia

The fear or dislike of advanced technology or complex devices, especially computers.

Inertia

Inertia is the resistance to change in state of motion or rest, applying to physical objects as well as to organizations and individuals' reluctance to change their behaviors or beliefs.

Related Questions

Q6: Referring to Table 16-5,the number of arrivals

Q14: Referring to Table 16-15,what is the Laspeyres

Q64: Using the best-subsets approach to model building,models

Q75: True or False: Referring to Table 14-17,there

Q114: Referring to Table 17-9,what is the p-value

Q117: Referring to Table 14-16,_ of the variation

Q134: True or False: When r = -1,it

Q158: Referring to Table 16-8,the fitted value for

Q267: Referring to Table 17-9,_ of the variation

Q293: Referring to Table 17-8,what is the p-value