Examlex

Solved

TABLE 15-4 the Superintendent of a School District Wanted to Predict the Predict

question 55

Multiple Choice

TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination ( TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
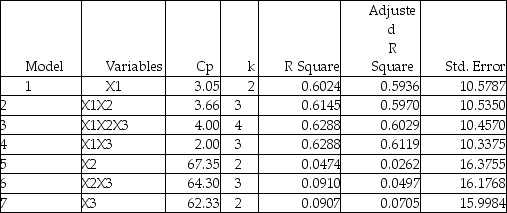The output from the best-subset regressions is given below: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. 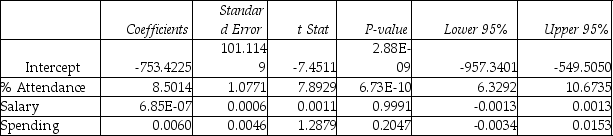Following is the residual plot for % Attendance: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. Following is the output of several multiple regression models:
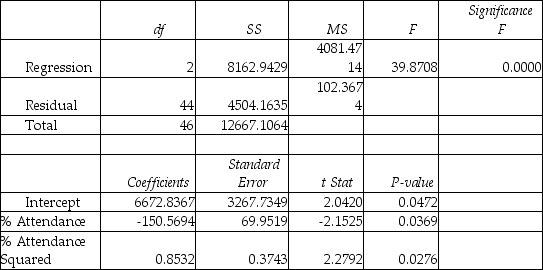
Model (I) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. Model (II) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. Model (III) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>.
-Referring to Table 15-4,the better model using a 5% level of significance derived from the "best" model above is

Definitions:

Final Number

The conclusive or ultimate figure that results from a series of calculations, measurements, or operations.

Customers

Individuals or entities that purchase goods or services produced by a business.

Lot Size

The number of units of product, shares, or other securities traded or manufactured in a single transaction or production run.

Inventory Level

The quantity of goods or materials on hand at a particular time within a business.

Related Questions

Q18: True or False: The Paasche price index

Q50: True or False: Referring to Table 15-6,the

Q60: Referring to Table 13-5,the standard error of

Q91: A second-order autoregressive model for average mortgage

Q129: Referring to Table 16-5,the number of arrivals

Q181: Referring to Table 13-3,the coefficient of correlation

Q189: Referring to Table 14-4,which of the following

Q191: Referring to Table 17-5,to test the significance

Q219: True or False: Referring to Table 14-15,you

Q235: Referring to Table 17-8,which of the following