TABLE 15-4 the Superintendent of a School District Wanted to Predict the Predict

question 43

True/False

TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X₁ = % Attendance,X₂ = Salaries and X₃ = Spending.
The coefficient of multiple determination ( )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below: 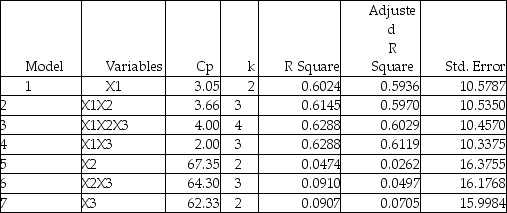Following is the residual plot for % Attendance: 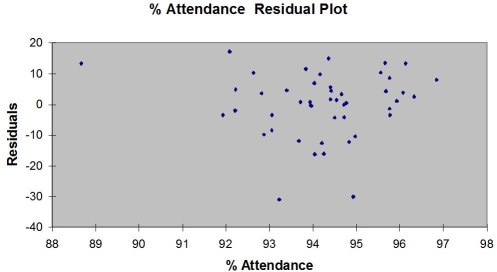Following is the output of several multiple regression models:
Model (I): 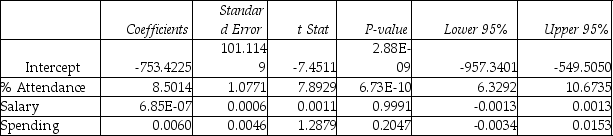Model (II): Model (III):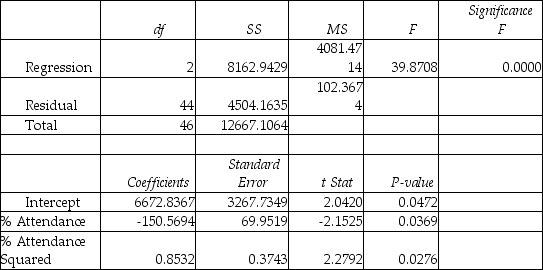
-True or False: Referring to Table 15-4,the null hypothesis should be rejected when testing whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance.

---

Definitions:

Rapid Breathing

An increased rate of respiration, which may occur due to exercise, stress, or medical conditions.

Internal Factor

An element within an organization or system that can affect its performance and outcomes.

Blood Pressure

The force exerted by circulating blood upon the walls of blood vessels, usually measured in the arteries.

Diastolic Pressure

The blood pressure measured when the heart relaxes.