Examlex

Solved

TABLE 15-4 the Superintendent of a School District Wanted to Predict the Predict

question 55

Multiple Choice

TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination ( TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
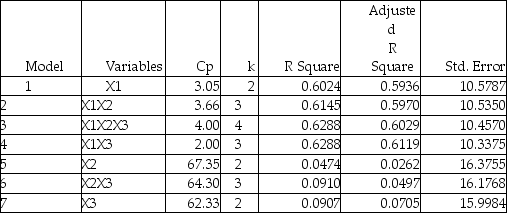The output from the best-subset regressions is given below: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. Following is the residual plot for % Attendance: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. Following is the output of several multiple regression models:
Model (I) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. Model (II) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>. Model (III) : TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) ,daily mean of the percentage of students attending class (% Attendance) ,mean teacher salary in dollars (Salaries) ,and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( ) of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I) : Model (II) : Model (III) : -Referring to Table 15-4,the better model using a 5% level of significance derived from the best model above is A) X<sub>1</sub>. B) X<sub>3</sub>. C) X<sub>1</sub>,X<sub>3</sub>. D) X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>.
-Referring to Table 15-4,the better model using a 5% level of significance derived from the "best" model above is

Definitions:

Creativity and Change

The process of implementing new ideas, methods, or innovations to initiate or respond to organizational, environmental, or market shifts.

Planning

The process of setting goals, developing strategies, and outlining tasks and schedules to achieve the objectives set.

Company's Objectives

are the specific, quantifiable targets set by a business aiming to guide its operations towards achieving its strategic goals.

Courses of Action

Refers to the different strategies or paths that can be taken to achieve a goal or solve a problem.

Related Questions

Q2: Referring to Table 15-1,does there appear to

Q17: Referring to Table 17-9,what is the correct

Q20: Referring to Table 14-4,what fraction of the

Q29: True or False: A high value of

Q61: True or False: The Chancellor of a

Q107: True or False: Referring to Table 14-16,the

Q131: Referring to Table 17-6,which of the following

Q137: Referring to Table 16-12,in testing the significance

Q137: Referring to Table 13-5,the partner wants to

Q300: Referring to Table 17-5,the estimated mean change