Examlex

Solved

TABLE 15-4 the Superintendent of a School District Wanted to Predict the Predict

question 79

True/False

TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X1 = % Attendance,X2 = Salaries and X3 = Spending.
The coefficient of multiple determination ( TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I): Model (II): Model (III): -True or False: Referring to Table 15-4,the residual plot suggests that a nonlinear model on % attendance may be a better model. )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
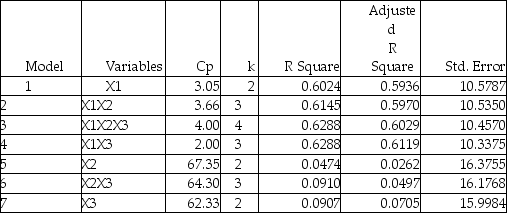The output from the best-subset regressions is given below: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I): Model (II): Model (III): -True or False: Referring to Table 15-4,the residual plot suggests that a nonlinear model on % attendance may be a better model. 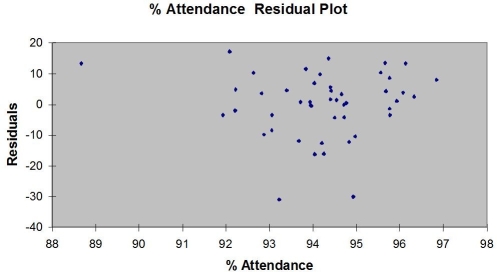Following is the residual plot for % Attendance: TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I): Model (II): Model (III): -True or False: Referring to Table 15-4,the residual plot suggests that a nonlinear model on % attendance may be a better model. Following is the output of several multiple regression models:
Model (I): TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I): Model (II): Model (III): -True or False: Referring to Table 15-4,the residual plot suggests that a nonlinear model on % attendance may be a better model. Model (II): TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I): Model (II): Model (III): -True or False: Referring to Table 15-4,the residual plot suggests that a nonlinear model on % attendance may be a better model. Model (III): TABLE 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Let Y = % Passing as the dependent variable,X<sub>1</sub> = % Attendance,X<sub>2</sub> = Salaries and X<sub>3</sub> = Spending. The coefficient of multiple determination ( )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743. The output from the best-subset regressions is given below: Following is the residual plot for % Attendance: Following is the output of several multiple regression models: Model (I): Model (II): Model (III): -True or False: Referring to Table 15-4,the residual plot suggests that a nonlinear model on % attendance may be a better model.
-True or False: Referring to Table 15-4,the residual plot suggests that a nonlinear model on % attendance may be a better model.

Definitions:

Residential Alcohol Rehabilitation

A live-in health care facility providing therapy for substance abuse disorders, specifically alcohol dependency.

Simultaneous Treatment

The process of providing multiple therapies or interventions at the same time to address different aspects of a condition.

Schizophrenia

A profound psychological condition marked by altered thoughts, feelings, perceptions, speech, self-awareness, and actions.

Cannabis Abuse

Misuse of cannabis leading to clinically significant impairment or distress.

Related Questions

Q26: True or False: The MAD is a

Q38: Referring to Table 16-8,the forecast for profits

Q61: Referring to Table 14-16,what is the value

Q65: Referring to Table 14-5,one company in the

Q79: Referring to Table 13-3,the director of cooperative

Q88: Referring to Table 17-12,what is the p-value

Q94: True or False: Each forecast using the

Q112: Referring to Table 14-5,what is the p-value

Q180: Referring to Table 13-3,the least squares estimate

Q186: True or False: The slopes in a