Examlex

Solved

TABLE 14-11 A Weight-Loss Clinic Wants to Use Regression Analysis to Build

question 175

Multiple Choice

TABLE 14-11
A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) . Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below:
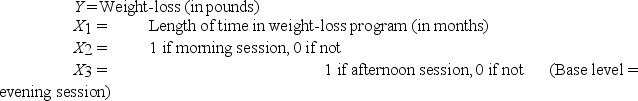TABLE 14-11 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) . Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below: Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: Partial output from Microsoft Excel follows: Regression Statistics ANOVA -Referring to Table 14-11, in terms of the β's in the model, give the average change in weight-loss (Y) for every 1 month increase in time in the program (X<sub>1</sub>) when attending the evening session. A) β<sub>1 </sub>+ β<sub>4</sub> B) β<sub>1 </sub>+ β<sub>5</sub> C) β<sub>1</sub> D) β<sub>4 </sub>+ β<sub>5</sub> Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
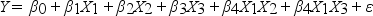TABLE 14-11 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) . Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below: Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: Partial output from Microsoft Excel follows: Regression Statistics ANOVA -Referring to Table 14-11, in terms of the β's in the model, give the average change in weight-loss (Y) for every 1 month increase in time in the program (X<sub>1</sub>) when attending the evening session. A) β<sub>1 </sub>+ β<sub>4</sub> B) β<sub>1 </sub>+ β<sub>5</sub> C) β<sub>1</sub> D) β<sub>4 </sub>+ β<sub>5</sub> Partial output from Microsoft Excel follows:
Regression Statistics
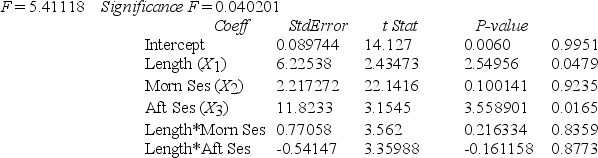
TABLE 14-11 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) . Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below: Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: Partial output from Microsoft Excel follows: Regression Statistics ANOVA -Referring to Table 14-11, in terms of the β's in the model, give the average change in weight-loss (Y) for every 1 month increase in time in the program (X<sub>1</sub>) when attending the evening session. A) β<sub>1 </sub>+ β<sub>4</sub> B) β<sub>1 </sub>+ β<sub>5</sub> C) β<sub>1</sub> D) β<sub>4 </sub>+ β<sub>5</sub> ANOVA
TABLE 14-11 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds) . Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below: Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: Partial output from Microsoft Excel follows: Regression Statistics ANOVA -Referring to Table 14-11, in terms of the β's in the model, give the average change in weight-loss (Y) for every 1 month increase in time in the program (X<sub>1</sub>) when attending the evening session. A) β<sub>1 </sub>+ β<sub>4</sub> B) β<sub>1 </sub>+ β<sub>5</sub> C) β<sub>1</sub> D) β<sub>4 </sub>+ β<sub>5</sub>
-Referring to Table 14-11, in terms of the β's in the model, give the average change in weight-loss (Y) for every 1 month increase in time in the program (X1) when attending the evening session.

Definitions:

Cost of Equity

The return a firm theoretically pays to its equity investors, i.e., shareholders, to compensate them for the risk they undertake by investing their capital.

Retained Earnings

The portion of a company's profits not distributed to shareholders as dividends but kept back to reinvest in the business.

DCF Approach

The Discounted Cash Flow (DCF) approach involves estimating the present value of an investment based on its expected future cash flows, adjusting for the cost of capital.

Cost of Equity

The rate of return a company is expected to pay to its shareholders to compensate them for the risk of investing in the company.

Related Questions

Q1: Referring to Table 14-4, at the 0.01

Q21: Referring to Table 15-5, what are, respectively,

Q25: Referring to Table 13-10, what is the

Q27: Referring to Table 14-13, the fitted model

Q45: Referring to Table 12-2, at 5% level

Q63: Referring to Table 11-6, the among group

Q84: A test for the difference between two

Q112: Referring to Table 16-6, exponential smoothing with

Q121: The confidence interval for the mean of

Q169: The slopes in a multiple regression model