Examlex

Solved

The Probabilities Shown in a Table with Two Rows

question 73

Multiple Choice

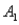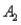The probabilities shown in a table with two rows, The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. and The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 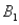and two columns, The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 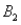and The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 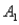,are as follows: P( The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 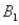and The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 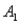) = 0.10,P( The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 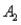and The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 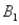) = 0.30,P( The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 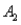and The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 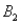) = 0.05,and P( The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. 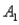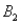and The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. ) = 0.55.Then P( The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. | The probabilities shown in a table with two rows, and and two columns, and ,are as follows: P( and ) = 0.10,P( and ) = 0.30,P( and ) = 0.05,and P( and ) = 0.55.Then P( | ) is A) 0.33. B) 0.35. C) 0.65. D) 0.67. ) is

Definitions:

Corporate Perspective

Corporate Perspective refers to the viewpoint or strategies adopted by a corporation in pursuit of its objectives, considering the interests of its stakeholders.

Divisional Perspective

A viewpoint focused on the specific goals, strategies, and performance of a distinct division within a larger company.

Share Options

Rights given to employees or investors to purchase shares of a company at a predetermined price for a specific period.

Performance-Related Pay

A compensation strategy that links employee salary or bonuses to their performance, aiming to motivate and reward employees for achieving specific business goals.

Related Questions

Q4: A regression analysis between X = sales

Q4: Research has shown that arrest works to

Q12: Aulette cited Ehrensaft who defined mothering as

Q15: A list of all members of the

Q25: What type of test is used to

Q26: As the sample size increases,the t-distribution becomes

Q27: A scatterplot that appears as a shapeless

Q30: In early America (before 1875)<br>A)there were no

Q30: A test for a population mean has

Q46: Veevers (cited by Aulette)interviewed married couples about