Number of Fish Tanks

question 18

Essay

Number of Fish Tanks
The following data give the number of fish tanks owned for a population of 4 families.

-{Number of Fish Tanks Narrative} A sample of size 2 is drawn at random from the population.Use the formulas and 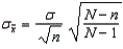to calculate the mean and the standard deviation of the sampling distribution of the sample means.

Recognize and name key phospholipids, such as cephalins and lecithins.

Understand the process of modifying lipid structures, such as converting phosphatidic acid to lecithin.

Explain how soaps and detergents function and differentiate between them.

Describe the structural features that allow phospholipids to form lipid bilayers.

---

Definitions:

Linear Optimization Model

A mathematical technique used to find the best outcome, such as maximum profit or lowest cost, in a model whose requirements are represented by linear relationships.

Outcomes

The possible results or consequences of a specific situation, experiment, or decision.

Reduced Cost

In linear programming, the amount by which the objective function coefficient of a variable must decrease before that variable's value increases in the optimal solution.

Bounded Variable

A variable that has upper and lower limits.