Robert Hope Received a Welcome Surprise in This Management Science $25 \%$

question 71

Essay

Robert Hope received a welcome surprise in this management science class; the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class. These instruments were: homework, an individual project, a mid-term exam, and a final exam. Robert's grades on these instruments were 75, 94, 85, and 92, respectively. However, the instructor complicated Robert's task somewhat by adding the following stipulations:
-homewark can account far up to $25 \%$ of the grade, but must be at least $5 \%$ af the grade;
- the praject can account for up to $25 \%$ of the grade, but must be at least $5 \%$ af the grade;
- the mid-term and final must each accaunt far betwen $10 \%$ and $40 \%$ of the grade but cannot accaunt far mare than $7 \%$ of the grade when the percentages are cambined; and
- the project and final exam grades may not collectively constitute more than $50 \%$ of the Iratade. The following LP model allows Robert to maximize his numerical grade.
$\begin{array} { l } \text { Let } \quad W _ { 1 } = \text { weight assigned to hamewark } \\ \quad \quad \quad W _ { \mathbf { 2 } } = \text { waight assigned to the praject } \\\quad \quad \quad W _ { 3 } = \text { weight assigned to the midi-term } \\ \quad \quad \quad W _ { 4 } = \text { waight assigned to the final } \\\\\text { MAX: } \quad 75 \mathrm {~W} _ { 1 } + 94 \mathrm {~W} _ { 2 } + 85 \mathrm {~W} _ { 3 } + 92 \mathrm {~W} _ { 4 } \\\text { Subject to: } \quad W _ { 1 } + W _ { 2 } + W _ { 3 } + W _ { 4 } = 1 \\ \quad \quad \quad \quad \quad \quad W _ { 3 } + W _ { 4 } \leq0 .70 \\ \quad \quad \quad \quad \quad \quad W _ { 3 } + W _ { 4 } \geq 0.50 \\ \quad \quad \quad \quad \quad \quad\text { 0. } 05 \leq W _ { 1 } \leq 0.25 \\ \quad \quad \quad \quad \quad \quad\text { 0. 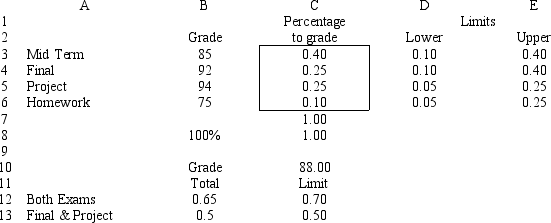} 05 \leq W _ { 2 } \leq 0.25 \\ \quad \quad \quad \quad \quad \quad\text { 0.10 } \leq W _ { 3 } \leq 0 .4 0 \\ \quad \quad \quad \quad \quad \quad0 .10 \leq W _ { 4 } \leq 0.40 \\\end{array}$ What values would you enter in the Risk Solver Platform (RSP) task pane for the cells in this Excel spreadsheet implementation of this problem?
Objective Cell:
Variables Cells:
Constraints Cells:

---

Definitions:

Alcohol Consumption

The act of drinking beverages containing ethanol, which can have various effects on health and behavior depending on the amount and frequency of intake.

Negative Correlation

A connection between two variables where one variable rises while the other falls.

Incidence of Dental Disease

Refers to the frequency or rate at which new cases of dental diseases occur in a population over a specified period of time.

Negative Correlation

A statistical relationship between two variables such that as one variable increases, the other decreases.