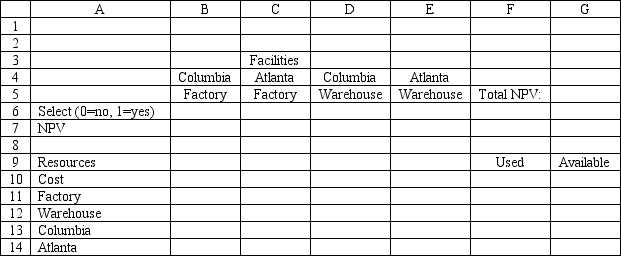
A Company Wants to Build a New Factory in Either

question 45

Essay

A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $15 million to invest.
$$\begin{array} { c l c c } \text { Variable } & \text { Decision } & \begin{array} { c } \text { NPV } \\(\text {\$ million } ) \end{array} & \begin{array} { c } \text { Cost } \\\text {\$ million } )\end{array} \\\hline \mathbf { X } _ { 1 } & \text { Factory in Columbia } & 3 & 10 \\\mathbf { X } _ { \mathbf { 2 } } & \text { Factory in Atlanta } & 4 & 8 \\\mathbf { X } _ { 3 } & \text { Warehouse in Columbia } & 2 & 0 \\\mathbf { X } _ { 4 } & \text { Warehouse in Atlanta } & 1 & 5\end{array}$$ Based on this ILP formulation of the problem and the indicated optimal solution what values should go in cells B6:G14 of the following Excel spreadsheet?
$\mathrm { MAX } : \quad 3 \mathbf { X } _ { 1 } + 4 \mathbf { X } _ { \mathbf { 2 } } + 2 \mathbf { X } _ { \mathbf { 3 } } + \mathbf { X } _ { 4 }$
Subject to:
$$\begin{array}{l}3 \mathrm{X}_{1}+4 \mathrm{X}_{2}+2 \mathrm{X}_{3}+\mathrm{X}_{4} \\10 \mathrm{X}_{1}+8 \mathrm{X}_{2}+6 \mathrm{X}_{3}+5 \mathrm{X}_{4} \leq 15 \\\mathrm{X}_{1}+\mathrm{X}_{2}=1 \\\mathrm{X}_{3}+\mathrm{X}_{4} \leq 1 \\\mathrm{X}_{3}-\mathrm{X}_{1} \leq 0 \\\mathrm{X}_{4}-\mathrm{X}_{2} \leq 0 \\\mathrm{X}_{\mathrm{i}}=0,1\end{array}$$
Solution: $\left(\mathrm{X}_{1}, \mathrm{X}_{2} \mathrm{X}_{3}, \mathrm{X}_{4}\right)=(0,1,0,1 )$

---

Definitions:

Neutral Self-Talk

The practice of engaging in inner dialogue that is neither overly positive nor negative, but rather objective and factual.

Overlearn

The process of continuing to study or practice beyond just mastering the material, to ensure longer-term retention.

Caffeinated Beverages

Drinks containing caffeine, a stimulant, which can boost alertness and energy levels.

Positive Self-Talk

The practice of making affirming statements to oneself, which can boost confidence, reduce stress, and improve overall mental health.