A Company Wants to Build a New Factory in Either

question 4

Essay

A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $16 million to invest.
$$\begin{array} { c l c c } \text { Variable } & \text { Decision } & \begin{array} { c } \text { NPV } \\\text { ( \$ million } ) \end{array} & \begin{array} { c } \text { Cost } \\\text { ( \$ million } )\end{array} \\\hline \mathbf { X } _ { 1 } & \text { Factory in Columbia } & 3 & 10 \\\mathbf { X } _ { \mathbf { 2 } } & \text { Factory in Atlanta } & 4 & 8 \\\mathbf { X } _ { 3 } & \text { Warehouse in Columbia } & 2 & 0 \\\mathbf { X } _ { 4 } & \text { Warehouse in Atlanta } & 1 & 5\end{array}$$ Based on this ILP formulation of the problem and the indicated optimal solution what formulas should go in cells F6:F14 of the following Excel spreadsheet?
$\mathrm { MAX } : \quad 3 \mathbf { X } _ { 1 } + 4 \mathbf { X } _ { \mathbf { 2 } } + 2 \mathbf { X } _ { \mathbf { 3 } } + \mathbf { X } _ { 4 }$
Subject to:
$$\begin{array} { l } 10 X _ { 1 } + \mathbf { 8 } X _ { \mathbf { 2 } } + 6 X _ { \mathbf { 3 } } + 5 \mathbf { X } _ { 4 } \leq 15 \\\mathbf { X } _ { 1 } + X _ { \mathbf { 2 } } = 1 \\\mathbf { X } _ { \mathbf { 3 } } + \mathbf { X } _ { \mathbf { 4 } } \leq 1 \\\mathbf { X } _ { \mathbf { 3 } } - \mathbf { X } _ { 1 } \leq 0 \\\mathbf { X } _ { \mathbf { 4 } } - \mathbf { X } _ { \mathbf { 2 } } \leq 0 \\\mathbf { X } _ { \mathrm { i } } = 0\end{array}$$
Solutian: $\left( \mathbf { X } _ { 1 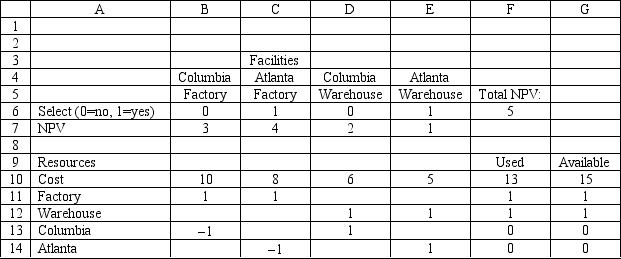} , \mathbf { X } _ { 2 } \mathbf { X } _ { \mathbf { y } } , \mathbf { X } _ { 4 } \right) = ( 0,1 ,0 , 1 )$

Understand the impact of foreign aid flow and its distribution among developing nations.

Understand the definition and characteristics of developing countries.

Identify and analyze the impact of direct foreign investment on economic growth in developing countries.

Evaluate the effectiveness of different types of foreign aid and development assistance policies.

---

Definitions:

Actuation Pressure

The minimum pressure required to operate or move a hydraulic or pneumatic component.

System Pressure

The force exerted by a fluid within a closed system, important for the operation of hydraulic and pneumatic systems.

Dual-Actuated Wedge Brakes

Braking systems that use two actuation mechanisms to apply pressure to a wedge, thus creating friction to slow or stop a vehicle.

Air-Actuated S-Cam Brakes

A type of brake system utilized in heavy vehicles where compressed air is used to rotate an S-shaped cam, applying the brakes.