A Company Wants to Build a New Factory in EitherBased on This ILP Formulation of the Problem and the Atlanta

The Answer of A Company Wants to Build a New Factory in EitherBased on This ILP Formulation of the Problem and the Atlanta

A Company Wants to Build a New Factory in EitherBased on This ILP Formulation of the Problem and the Atlanta

The Answer of A Company Wants to Build a New Factory in EitherBased on This ILP Formulation of the Problem and the Atlanta

Solved

A Company Wants to Build a New Factory in Either

question 45

Essay

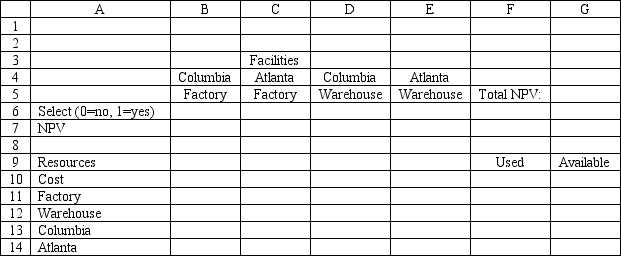
A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $15 million to invest.
$\begin{array} { c l c c } \text { Variable } & \text { Decision } & \begin{array} { c } \text { NPV } \\(\text {\$ million } ) \end{array} & \begin{array} { c } \text { Cost } \\\text {\$ million } )\end{array} \\\hline \mathbf { X } _ { 1 } & \text { Factory in Columbia } & 3 & 10 \\\mathbf { X } _ { \mathbf { 2 } } & \text { Factory in Atlanta } & 4 & 8 \\\mathbf { X } _ { 3 } & \text { Warehouse in Columbia } & 2 & 0 \\\mathbf { X } _ { 4 } & \text { Warehouse in Atlanta } & 1 & 5\end{array}$ Based on this ILP formulation of the problem and the indicated optimal solution what values should go in cells B6:G14 of the following Excel spreadsheet?
$\mathrm { MAX } : \quad 3 \mathbf { X } _ { 1 } + 4 \mathbf { X } _ { \mathbf { 2 } } + 2 \mathbf { X } _ { \mathbf { 3 } } + \mathbf { X } _ { 4 }$
Subject to:
$\begin{array}{l}3 \mathrm{X}_{1}+4 \mathrm{X}_{2}+2 \mathrm{X}_{3}+\mathrm{X}_{4} \\10 \mathrm{X}_{1}+8 \mathrm{X}_{2}+6 \mathrm{X}_{3}+5 \mathrm{X}_{4} \leq 15 \\\mathrm{X}_{1}+\mathrm{X}_{2}=1 \\\mathrm{X}_{3}+\mathrm{X}_{4} \leq 1 \\\mathrm{X}_{3}-\mathrm{X}_{1} \leq 0 \\\mathrm{X}_{4}-\mathrm{X}_{2} \leq 0 \\\mathrm{X}_{\mathrm{i}}=0,1\end{array}$
Solution: $\left(\mathrm{X}_{1}, \mathrm{X}_{2} \mathrm{X}_{3}, \mathrm{X}_{4}\right)=(0,1,0,1 )$

$A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $15 million to invest. \begin{array} { c l c c } \text { Variable } & \text { Decision } & \begin{array} { c } \text { NPV } \\ (\text {\$ million } ) \end{array} & \begin{array} { c } \text { Cost } \\ \text {\$ million } ) \end{array} \\ \hline \mathbf { X } _ { 1 } & \text { Factory in Columbia } & 3 & 10 \\ \mathbf { X } _ { \mathbf { 2 } } & \text { Factory in Atlanta } & 4 & 8 \\ \mathbf { X } _ { 3 } & \text { Warehouse in Columbia } & 2 & 0 \\ \mathbf { X } _ { 4 } & \text { Warehouse in Atlanta } & 1 & 5 \end{array} Based on this ILP formulation of the problem and the indicated optimal solution what values should go in cells B6:G14 of the following Excel spreadsheet? \mathrm { MAX } : \quad 3 \mathbf { X } _ { 1 } + 4 \mathbf { X } _ { \mathbf { 2 } } + 2 \mathbf { X } _ { \mathbf { 3 } } + \mathbf { X } _ { 4 } Subject to: \begin{array}{l} 3 \mathrm{X}_{1}+4 \mathrm{X}_{2}+2 \mathrm{X}_{3}+\mathrm{X}_{4} \\ 10 \mathrm{X}_{1}+8 \mathrm{X}_{2}+6 \mathrm{X}_{3}+5 \mathrm{X}_{4} \leq 15 \\ \mathrm{X}_{1}+\mathrm{X}_{2}=1 \\ \mathrm{X}_{3}+\mathrm{X}_{4} \leq 1 \\ \mathrm{X}_{3}-\mathrm{X}_{1} \leq 0 \\ \mathrm{X}_{4}-\mathrm{X}_{2} \leq 0 \\ \mathrm{X}_{\mathrm{i}}=0,1 \end{array} Solution: \left(\mathrm{X}_{1}, \mathrm{X}_{2} \mathrm{X}_{3}, \mathrm{X}_{4}\right)=(0,1,0,1 )$

Definitions:

Sales Presentation

A pitch or demonstration given to potential buyers highlighting the benefits and features of a product or service.

Approach Phase

The initial stage in the sales process where the salesperson first contacts the potential customer, aiming to establish rapport and understand customer needs.

Building Rapport

The process of establishing a connection or trust with someone, essential in sales to facilitate open communication and understanding.

Customer Benefit Plan

A strategic offering designed to provide additional value to customers, often through services or rewards, to enhance customer satisfaction and loyalty.