A Company Wants to Build a New Factory in Either

question 4

Essay

A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $16 million to invest.
$$\begin{array} { c l c c } \text { Variable } & \text { Decision } & \begin{array} { c } \text { NPV } \\\text { ( \$ million } ) \end{array} & \begin{array} { c } \text { Cost } \\\text { ( \$ million } )\end{array} \\\hline \mathbf { X } _ { 1 } & \text { Factory in Columbia } & 3 & 10 \\\mathbf { X } _ { \mathbf { 2 } } & \text { Factory in Atlanta } & 4 & 8 \\\mathbf { X } _ { 3 } & \text { Warehouse in Columbia } & 2 & 0 \\\mathbf { X } _ { 4 } & \text { Warehouse in Atlanta } & 1 & 5\end{array}$$ Based on this ILP formulation of the problem and the indicated optimal solution what formulas should go in cells F6:F14 of the following Excel spreadsheet?
$\mathrm { MAX } : \quad 3 \mathbf { X } _ { 1 } + 4 \mathbf { X } _ { \mathbf { 2 } } + 2 \mathbf { X } _ { \mathbf { 3 } } + \mathbf { X } _ { 4 }$
Subject to:
$$\begin{array} { l } 10 X _ { 1 } + \mathbf { 8 } X _ { \mathbf { 2 } } + 6 X _ { \mathbf { 3 } } + 5 \mathbf { X } _ { 4 } \leq 15 \\\mathbf { X } _ { 1 } + X _ { \mathbf { 2 } } = 1 \\\mathbf { X } _ { \mathbf { 3 } } + \mathbf { X } _ { \mathbf { 4 } } \leq 1 \\\mathbf { X } _ { \mathbf { 3 } } - \mathbf { X } _ { 1 } \leq 0 \\\mathbf { X } _ { \mathbf { 4 } } - \mathbf { X } _ { \mathbf { 2 } } \leq 0 \\\mathbf { X } _ { \mathrm { i } } = 0\end{array}$$
Solutian: 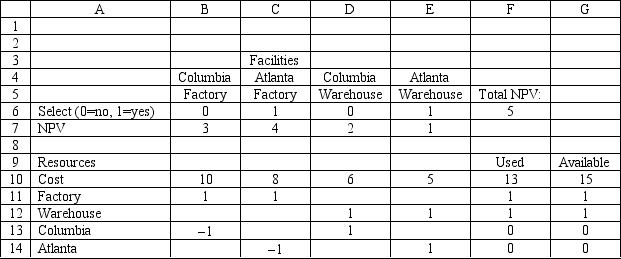$\left( \mathbf { X } _ { 1 } , \mathbf { X } _ { 2 } \mathbf { X } _ { \mathbf { y } } , \mathbf { X } _ { 4 } \right) = ( 0,1 ,0 , 1 )$

---

Definitions:

Positive Reinforcement

A behavioral strategy that involves rewarding a behavior to increase the likelihood of that behavior being repeated.

Observational Learning

The process of acquiring new behaviors or knowledge by watching and imitating others.

Classical Conditioning

Modifying behavior by pairing a conditioned stimulus with an unconditioned stimulus to elicit an unconditioned response.

Respondent Conditioning

A form of learning in which a behavioral response is elicited by a previously neutral stimulus that has become associated with a meaningful stimulus.