Exhibit 10 $\text {Discriminant Analysis Report}$ $\quad$ $\quad$ $\quad$

question 55

Essay

Exhibit 10.5
The information below is used for the following questions.
A counselor wants to classify people as belonging to one of three groups based on two scores. The counselor has collected data on twenty people who are known to be in one of the three groups. The data for the problem are in the following spreadsheet. Output generated using Risk Solver Platform (RSP) is also included.
$\text {Discriminant Analysis Report}$
$\quad$$\quad$$\quad$$\quad$$\text {October 3,2010}$$\quad$$\quad$$\text { 5:56:34 PM}$
$\text {Unpooled Estimates of within-group Covariance matrices are used, assuming they are differen}$

$\text { Group Centroids }$

$\begin{array}{crr}\text { Group } & \mathrm{X} 1 & \mathrm{X} 2 \\\hline 1 & 242 & 148.8333333 \\2 & 237.8571429 & 149.1428571 \\3 & 2328571420 & 1411428571\end{array}$
$\text { Group Frequencies }$
$\begin{array}{cr}&\text { Relative }\\\text { Group } & \text { Frequency } \\\hline 1 & 30.00 \% \\2 & 35.00 \% \\3 & 3500 \%\end{array}$

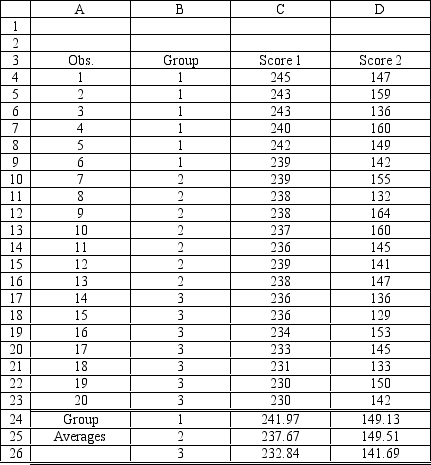
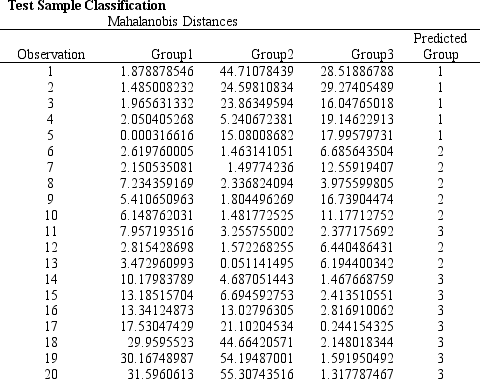
-Refer to Exhibit 10.5. Based on the 20 observations in the model complete the following confusion/classification matrix.
$\begin{array}{lllll}\text { Actual } & \text { Group 1 } & \text { Group 2 } & \text { Group } 3 & \text { Total } \\\hline \text { Group } 1 & & & \\\text { Group } 2 & & & \\\text { Group } 3 & & & \\\text { Total } & & &\\\\\text { \% Correct }&&\end{array}$

---

Definitions:

Outliers

Data points that differ significantly from the majority of a data set, often indicating a variance or error in measurement.

Variability

The tendency of data points in a dataset to vary from each other and from the mean of the dataset.

Mode

The value that appears most frequently in a data set, representing the highest peak in a frequency distribution.

Standard Deviation

A statistical measure that quantifies the amount of variation or dispersion of a set of data values from the mean.