Exhibit 12.5
The following questions use the information below.
The owner of Sal's Italian Restaurant wants to study the growth of his business using simulation. He is interested in simulating the number of customers and the amount ordered by customers each month. He currently serves 1000 customers per month and feels this can vary uniformly between a decrease of as much as 5% and an increase of up to 9%. The bill for each customer is a normally distributed random variable with a mean of $20 and a standard deviation of $5. The average order has been increasing steadily over the years and the owner expects the mean order will increase by 2% per month. You have created the following spreadsheet to simulate the problem.
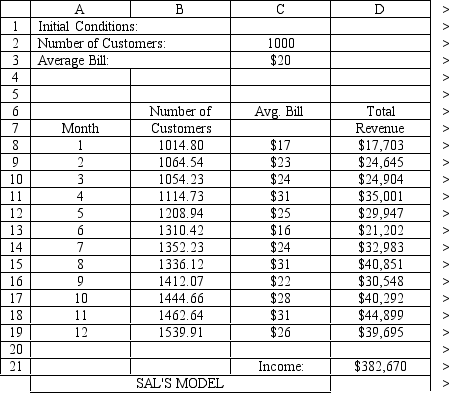
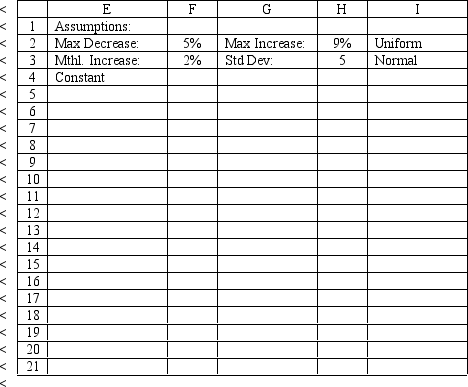
-Sal, from Exhibit 12.5, has produced the following spreadsheet to compute confidence intervals on his income. What formula should go in cell B8 to compute the upper limit on a 95% confidence interval for the true population mean?
Definitions:
Q6: One role of holding inventory is to
Q6: Why do we create a scatter plot
Q10: Refer to Exhibit 14.4. What is the
Q11: Suppose that the first goal in a
Q15: A manager wants to ensure that he
Q16: The FCFS rule is most often used
Q24: Refer to Exhibit 14.8. The Consistency Ratio
Q34: Which oneof the following is an example
Q45: Refer to Exhibit 15.3. The following
Q49: Refer to Exhibit 7.1. If the company