Project 12.1- Monte Carlo Integration

question 6

Essay

Project 12.1- Monte Carlo Integration
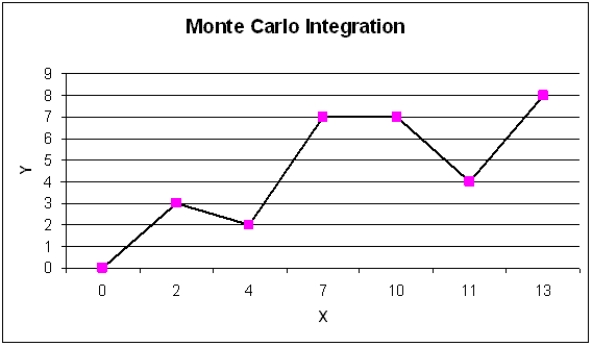
A common application of Monte Carlo simulation is to provide numerical approximations. One such application is to approximate the area under a curve, or Monte Carlo integration. The following figure represents such a curve, defined over the range of X = 0 to X = 13. Call the area under this curve A.
Monte Carlo integration begins by overlaying on the curve of interest a region (call this region, B) whose area is easy to calculate (i.e., a box). Monte Carlo integration then involves the random generation of points in B and a determination of the percentage of these points that fall in A (i.e., fall below the curve). This percentage represents that portion of the area of B that is the area of A.
Use Monte Carlo integration techniques to approximate the area under the curve. Use exact techniques to calculate the true area under the curve. How accurate is your approximation?

---

Definitions:

Total Logistics Costs

The cumulative expenses associated with the planning, implementing, and controlling of the movement and storage of goods and services from their point of origin to their point of consumption.

Transportation Costs

The expenses associated with the movement of goods or passengers from one location to another.

Facility Costs

Expenses related to the physical buildings and infrastructure used in the manufacturing, storage, and distribution processes in a supply chain.

Flexible Technology

Technology that can be easily adapted or adjusted to support varying operational or production requirements.