Exhibit 12

question 47

Short Answer

Exhibit 12.5
The following questions use the information below.
The owner of Sal's Italian Restaurant wants to study the growth of his business using simulation. He is interested in simulating the number of customers and the amount ordered by customers each month. He currently serves 1000 customers per month and feels this can vary uniformly between a decrease of as much as 5% and an increase of up to 9%. The bill for each customer is a normally distributed random variable with a mean of $20 and a standard deviation of $5. The average order has been increasing steadily over the years and the owner expects the mean order will increase by 2% per month. You have created the following spreadsheet to simulate the problem.

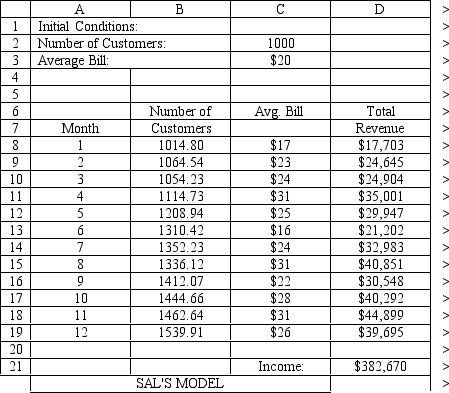
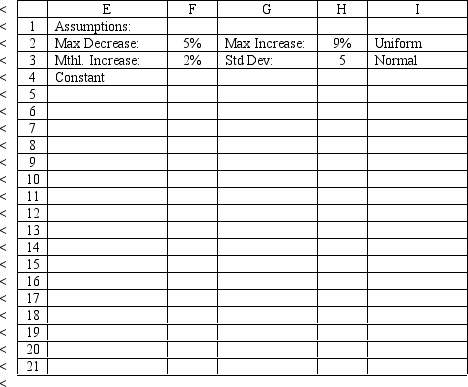
-Sal, from Exhibit 12.5, has produced the following spreadsheet to compute confidence intervals on his income. What formula should go in cell B12 to compute the upper limit on a 95% confidence interval for the population proportion below 90%?
$$\begin{array} { | c | l | c | } \hline &{ \text { A } } & \text { B } \\\hline 1 & & \\\hline 2 & \text { Sample Size: } & 300 \\\hline 3 & & \\\hline 4 & \text { Sample Mean: } & 4,119,519 \\\hline 5 & \text { Sample Standard Deviation: } & 291,117 \\\hline 6 & & \\\hline 7 & 95 \% \text { LCL far the papulation mean: } & 4,086,576 \\\hline 8 & 95 \% \text { UCL far the population mean: } & 4,152,462 \\\hline 9 & & \\\hline 10 & \text { Target Prapartion } & 0.900 \\\hline 11 & 95 \% \text { Lower Confidence Linnit: } & 0.866 \\\hline 12 & 95 \% \text { Upper Confidence I.init: } & 0.934 \\\hline\end{array}$$

Identify symptoms and interventions for posttraumatic stress disorder (PTSD).

Appreciate the role of relaxation techniques in managing stress and trauma responses.

Recognize events likely to precipitate PTSD and understand the variability of trauma responses.

Understand the concept of media richness and its implications for communication effectiveness.