The Brakes on a Bicycle Are Applied by Using a Downward

question 161

Multiple Choice

The brakes on a bicycle are applied by using a downward force of p pounds on the pedal when the six-inch crank makes a angle with the horizontal.Vectors representing the position of the crank and the force are $$\mathbf { V } = \frac { 1 } { 6 } \left( - \cos 70 ^ { \circ } \mathbf { j } - \sin 70 ^ { \circ } \mathbf { k } \right)$$ and $$\mathbf { F } = - p \mathbf { k }$$ respectively.The magnitude of the torque on the crank is given by $$\| \mathbf { V } \times \mathbf { F } \|$$ .Using the given information,write the torque T on the crank as a function of p.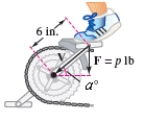

• A) \(T = - \frac { p } { 5 } \sin 70 ^ { \circ }\)
• B) \(T = \frac { p } { 3 } \cos 70 ^ { \circ }\)
• C) \(T = - \frac { p } { 5 } \cos 70 ^ { \circ }\)
• D) \(T = \frac { 1 } { 5 } \cos 70 ^ { \circ }\)
• E) \(T = \frac { p } { 5 } \sin 70 ^ { \circ }\)

---

Definitions:

Business Strategy

It's a plan of action designed by business leaders to achieve competitive advantage and successfully compete in the market.

Average Total Cost

The total cost of production divided by the number of units produced, indicating the average cost per unit of output.

Competitive Market

An economic scenario where numerous producers and consumers interact, ensuring prices are determined by supply and demand forces without significant influence by any single participant.

Sunk Costs

Expenses that have been incurred and cannot be recovered, regardless of future actions.