TABLE 15-9
Many factors determine the attendance at Major League Baseball games. These factors can include when the game is played, the weather, the opponent, whether or not the team is having a good season, and whether or not a marketing promotion is held. Data from 80 games of the Kansas City Royals for the following variables are collected.
ATTENDANCE = Paid attendance for the game
TEMP = High temperature for the day
WIN% = Team's winning percentage at the time of the game
OPWIN% = Opponent team's winning percentage at the time of the game WEEKEND - 1 if game played on Friday, Saturday or Sunday; 0 otherwise PROMOTION - 1 = if a promotion was held; 0 = if no promotion was held
The regression results using attendance as the dependent variable and the remaining five variables as the independent variables are presented below.
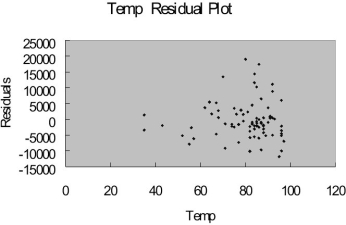
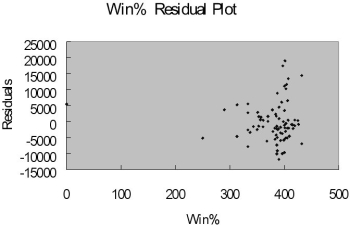
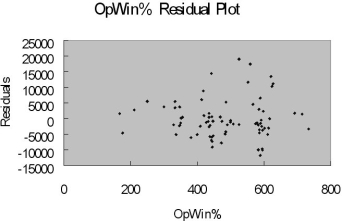
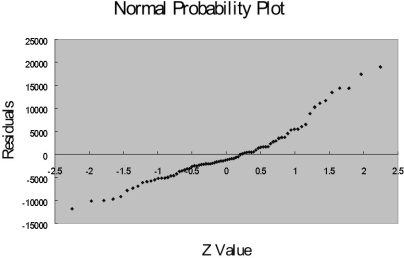
The coefficient of multiple determination ( R 2 j ) of each of the 5 predictors with all the other remaining predictors are,
respectively, 0.2675, 0.3101, 0.1038, 0.7325, and 0.7308.
-Referring to Table 15-9,_____ of the variation in ATTENDANCE can be explained by the five independent variables after taking into consideration the number of independent variables and the number of observations.
Definitions:
Legislation
Laws that have been enacted by a legislative body, such as a parliament or congress.
Physical Threats
Explicit or implicit actions suggesting the intent to cause bodily harm to another person.
Collection Agency
A business that pursues payments of debts owed by individuals or businesses on behalf of creditors.
Demand for Payment
A formal request made by a creditor to a debtor requiring the latter to pay an outstanding debt by a specified deadline.
Q8: A realtor wants to compare the variability
Q13: Referring to Table 15-8, the quadratic effect
Q30: Referring to Table 14-4, what are the
Q32: Referring to Table 18-4, suppose the supervisor
Q42: Referring to Table 14-17, what should be
Q54: Referring to Table 13-4, the error or
Q56: _causes of variation are correctable without modifying
Q62: Using the best-subsets approach to model building,
Q110: Referring to Table 18-7, an R chart
Q117: If the plot of the residuals is