TABLE 15-9
Many factors determine the attendance at Major League Baseball games. These factors can include when the game is played, the weather, the opponent, whether or not the team is having a good season, and whether or not a marketing promotion is held. Data from 80 games of the Kansas City Royals for the following variables are collected.
ATTENDANCE = Paid attendance for the game
TEMP = High temperature for the day
WIN% = Team's winning percentage at the time of the game
OPWIN% = Opponent team's winning percentage at the time of the game WEEKEND - 1 if game played on Friday, Saturday or Sunday; 0 otherwise PROMOTION - 1 = if a promotion was held; 0 = if no promotion was held
The regression results using attendance as the dependent variable and the remaining five variables as the independent
variables are presented below.
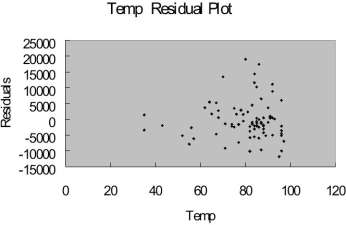
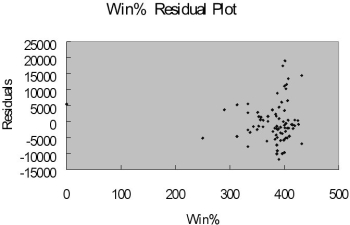
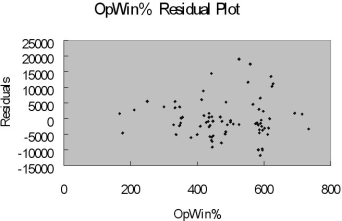
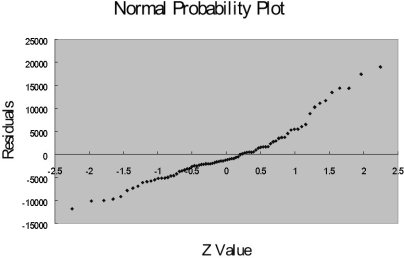
The coefficient of multiple determination ( R 2 j) of each of the 5 predictors with all the other remaining predictors are, respectively, 0.2675, 0.3101, 0.1038, 0.7325, and 0.7308.
-Referring to Table 15-9, there is enough evidence to conclude that TEMP makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance.
Definitions:
Adverse Events
Unintended harm or complications resulting from medical treatment or procedures.
Time Management
The ability to use one's time effectively or productively, especially at work or in daily activities.
Competing Priorities
Situations where two or more tasks or demands are simultaneously required, necessitating prioritization and efficient time management.
Laissez-Faire
An economic philosophy of free-market capitalism that opposes government intervention.
Q8: Referring to Table 13-12, the model appears
Q30: Referring to Table 14-4, what are the
Q40: Referring to Table 13-1, interpret the estimate
Q62: Referring to Table 14-3, to test whether
Q84: Referring to Table 16-6, exponential smoothing with
Q90: Referring to Table 17-6, the optimal strategy
Q105: Referring to Table 17-5, what is the
Q106: Referring to Table 16-6, the Holt-Winters method
Q170: Referring to Table 13-3, suppose the director
Q191: Referring to Table 16-14, what is the