Solved

TABLE 13-12
the Manager of the Purchasing Department of a Large

question 77

Multiple Choice

TABLE 13-12
The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output:
$\begin{array}{l}\text { Regression Statistics }\\\begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\\text { R Square } & 0.8924 \\\text { Adjusted R Square } & 0.8886 \\\text { Standard Error } & 0.3342 \\\text { ations } & 30 \\\hline\end{array}\end{array}$

$\begin{array}{lrrccc}\hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\\hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrr}\hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\\hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\\hline\end{array}$

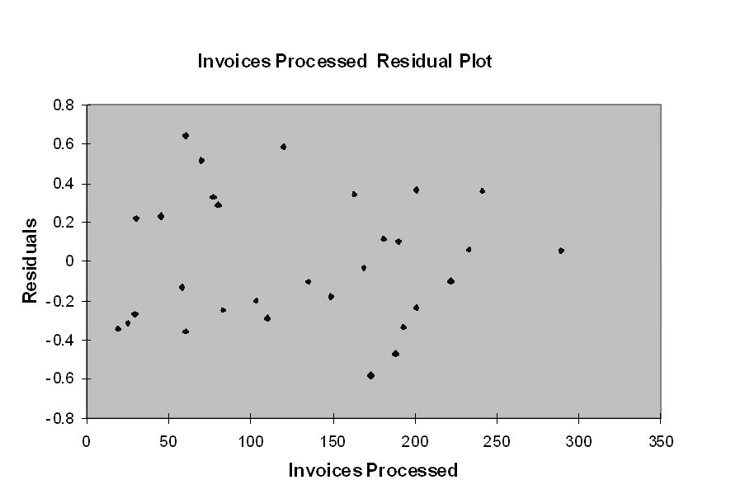
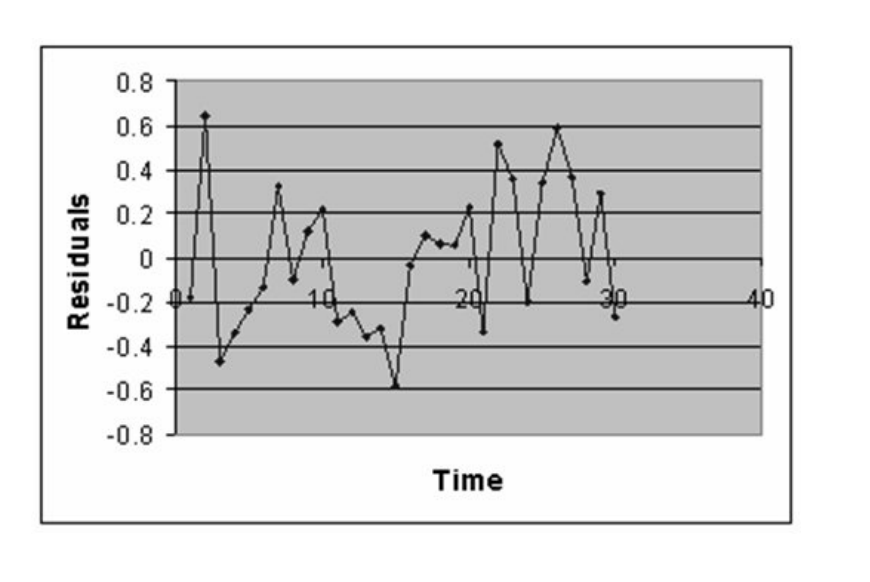
$TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{l} \text { Regression Statistics }\\ \begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { ations } & 30 \\ \hline \end{array} \end{array} \begin{array}{lrrccc} \hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\ \hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\ \hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, the error sum of squares (SSE) of the above regression is A) 0.1117. B) 29.0720. C) 25.9438. D) 3.1282.$

$TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{l} \text { Regression Statistics }\\ \begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { ations } & 30 \\ \hline \end{array} \end{array} \begin{array}{lrrccc} \hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\ \hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\ \hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, the error sum of squares (SSE) of the above regression is A) 0.1117. B) 29.0720. C) 25.9438. D) 3.1282.$

-Referring to Table 13-12, the error sum of squares (SSE) of the above regression is

Definitions:

Depth

The measurement from the top surface to the bottom in an object, often used to specify the extent of features such as holes or cuts.

Third Dimension

The third dimension adds depth to two-dimensional representations, enabling the portrayal of length, width, and height or depth, thus offering a more comprehensive visualization.

Separate Drawing

An individual drawing sheet that details a single part or component, used for clarity or to specify complex details, separate from the main assembly drawing.

Drafting Time

The duration spent preparing technical drawings and detailed plans in engineering, architecture, or related fields.

TABLE 13-12 the Manager of the Purchasing Department of a Large

Definitions:

TABLE 13-12
the Manager of the Purchasing Department of a Large