TABLE 13- 11
a Company That Has the Distribution Rights

question 155

True/False

TABLE 13- 11
A company that has the distribution rights to home video sales of previously released movies would like to use the box office gross (in millions of dollars) to estimate the number of units (in thousands of units) that it can expect to sell. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different movie titles:
$$\begin{array}{l}\text { Regression Statistics }\\\begin{array} { l c } \hline \text { Multiple R } & 0.8531 \\\text { RSquare } & 0.7278 \\\text { Adjusted R Square } & 0.7180 \\\text { Standard Error } & 47.8668 \\\text { Observations } & 30\end{array}\end{array}$$
ANOVA
$\begin{array}{lrrrrr}\hline &\text { d f}& \text { SS } & \text { MS } & \text {F }& \text {Significance F} \\\hline \text {Regression }& 1 & 171499.78 & 171499.78 & 74.8505 & 2.1259E-09 \\\text {Residual} & 28 & 64154.42 & 2291.23 & & \\\text {Total} & 29 & 235654.20 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrr}\hline & \text {Coefficients }& \text { Standard Error}& \text { t Stat }& \text { p -value }& \text {Lower 95\% }& \text {Upper 95\% }\\\hline \text { Intercept }& 76.5351 & 11.8318 & 6.4686 & 5.24 \mathrm{E}-07& 52.2987 & 100.7716 \\ \text {Gross} & 4.3331 & 0.5008 & 8.6516 & 2.13 \mathrm{E}-09 & 3.3072 & 5.3590 \\\hline\end{array}$



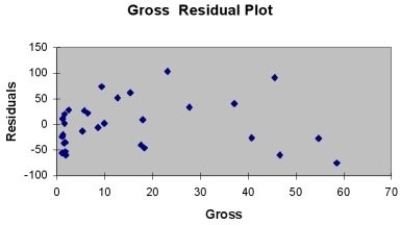
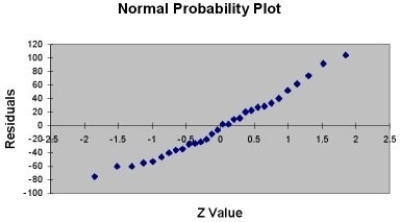
TABLE 13-5
$\begin{array}{lc}\hline \text {Regression Statistics } \\\hline \text { Multiple R} & 0.802 \\ \text {R Square} & 0.643 \\ \text {Adjusted R Square} & 0.618 \\ \text {Standard Error SYX }& 0.9224 \\ \text {Observations} & 16 \\\hline\end{array}$

ANOVA
$\begin{array}{lrlrlr}\hline & \text {d f } & \text { SS} & \text { MS } & \text {F } & \text { Sig.F }\\\hline \text { Regression }& 1 & 21.497 & 21.497 & 25.27 & 0.000 \\ \text {Error }& 14 & 11.912 & 0.851 & & \\ \text {Total }& 15 & 33.409 & & & \\\hline\end{array}$

$\begin{array}{lllrr}\hline \text {Predictor} & \text {Coefficients} &\text { Standard Error }&\text { t Stat }& \text { p -value} \\\hline \text {Intercept} & 3.962 & 1.440 & 2.75 & 0.016 \\\text {Industry} & 0.040451 & 0.008048 & 5.03 & 0.000 \\\hline\end{array}$
-Referring to Table 13-11, the null hypothesis that there is no linear relationship between box office gross and home video unit sales should be reject at a 5% level of significance.

---

Definitions:

Welcoming Attitude

A demeanor or approach characterized by openness, friendliness, and readiness to receive and accept others warmly.

Bill Gates

An American business magnate, software developer, and philanthropist, best known as the co-founder of Microsoft Corporation.

High-quality Customer Service

The act of providing exceptional service to customers, ensuring their satisfaction and loyalty.

Cornerstones

Fundamental principles or elements on which something is based or constructed.