Examlex

Solved

Suppose That a Recent Study Shows That Each Week Each

question 6

Essay

Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) denote the probability that a gallon produced by company A is of unsatisfactory quality, and define Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. 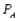(Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) and Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands.
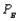-After a year, what will the market share for each of the three companies be? Assume Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. 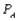(Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) = 0.10, Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. 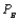(Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) = 0.15, and Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. 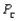(Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.)

Definitions:

Unit Product Cost

The cost incurred to produce, manufacture, or acquire a single unit of a product.

Predetermined Overhead Rate

A rate calculated at the beginning of a period, used to allocate estimated overhead to individual products or job orders based on a specific activity base.

Manufacturing Departments

Specific divisions within a manufacturing facility, each responsible for different aspects of the production process.

Predetermined Overhead Rates

A rate calculated before a period begins, used to allocate manufacturing overhead costs to products based on a selected activity base, such as machine-hours.

Related Questions

Q7: Write out an algebraic expression for the

Q31: Transportation costs for a given route are

Q37: If the standard deviations of X and

Q45: It helps to ensure that Solver can

Q62: The flows in a general minimum cost

Q67: What is an example of a financial

Q81: Which of the following is not one

Q82: There are two types of random variables,

Q92: Which of the following best describes the

Q96: Proportionality, additivity, and divisibility are three important