Examlex

Solved

Suppose That a Recent Study Shows That Each Week Each

question 6

Essay

Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let 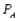denote the probability that a gallon produced by company A is of unsatisfactory quality, and define 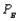and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume 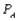= 0.10, 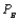= 0.15, and 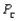= 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) denote the probability that a gallon produced by company A is of unsatisfactory quality, and define Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) and Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands.
-After a year, what will the market share for each of the three companies be? Assume Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) = 0.10, Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) = 0.15, and Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let denote the probability that a gallon produced by company A is of unsatisfactory quality, and define and similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands. -After a year, what will the market share for each of the three companies be? Assume = 0.10, = 0.15, and = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.) = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.)

Explain the role of social influence in shaping perceptions, attitudes, and actions.
Understand the psychological and neural responses to conforming or not conforming to group norms.
Understand the distinction and interaction between cognitive and mechanical processes in conditioning.
Identify the roles and effects of models in observational learning.

Definitions:

Retained Earnings

The portion of a company's profits not distributed as dividends to shareholders, but instead reinvested in the business or held as reserves.

Assets

Assets are resources owned by a business or individual, which provide economic value or are expected to generate future benefit.

Revenues

The income generated from normal business operations and includes discounts and deductions for returned merchandise.

Limited Liability

A legal structure that limits the financial liability of owners or shareholders of a business to the amount they've invested, protecting personal assets from business debts.

Related Questions

Q18: Correlation and covariance measure:<br>A) the strength of

Q29: If the random variable X is exponentially

Q30: It is often useful to perform sensitivity

Q36: There are two primary ways to formulate

Q38: Simulate Amanda's portfolio over the next 30

Q47: Simulate Amanda's portfolio over the next 30

Q60: Much of the study of probabilistic inventory

Q71: Comparing a numerical variable across two or

Q79: Explain why the mean is slightly lower

Q88: Your friend is moving from Michigan to