A Manufacturing Firm Wants to Determine Whether a Relationship Exists

question 74

Essay

A manufacturing firm wants to determine whether a relationship exists between the number of work-hours an employee misses per year (Y) and the employee's annual wages (X), to test the hypothesis that increased compensation induces better work attendance. The data provided in the table below are based on a random sample of 15 employees from this organization.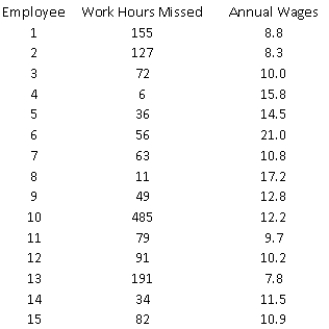
-(A) Estimate a simple linear regression model using the sample data. How well does the estimated model fit the sample data?
​
(B) Perform an F-test for the existence of a linear relationship between Y and X. Use a 5% level of significance.
​
(C) Plot the fitted values versus residuals associated with the model. What does the plot indicate?
​
(D) How do you explain the results you have found in (A) through (C)?
​
(E) Suppose you learn that the 10^th employee in the sample has been fired for missing an excessive number of work-hours during the past year. In light of this information, how would you proceed to estimate the relationship between the number of work-hours an employee misses per year and the employee's annual wages, using the available information? If you decide to revise your estimate of this regression equation, repeat (A) and (B)

---

Definitions:

Resistance To Change

The opposition or reluctance to modify or abandon traditional practices or to adapt to new ones.

Dramatic Increase

A significant and rapid rise in numbers, magnitude, or extent of a particular phenomenon or metric.

Kurt Lewin

is known as the father of modern social psychology, who developed theories on group dynamics and organizational development.

Force Field Analysis

A method developed by Kurt Lewin to analyze the factors that support or hinder a particular situation or desired change by identifying and evaluating driving and restraining forces.