Set Up the System of Equations and Then Solve It

question 225

Multiple Choice

Set up the system of equations and then solve it by using inverse matrices. ​
Bee ancestry Because a female bee comes from a fertilized egg and a male bee comes from an unfertilized egg, the number of ancestors of a male t + 2 bee generations before the present generation is the sum of the number of ancestors t and t + 1 generations before the present. If the numbers of ancestors of a male bee in a given generation t and in the previous generation are given by 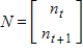, then there is a matrix M such that the numbers of ancestors in the two generations preceding generation t are given by .
​
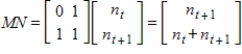For a given male bee, the numbers of ancestors 5 and 6 generations back are given by .
​
Find the numbers of ancestors 4 and 5 generations back by multiplying both sides of by the inverse of M.
​

Explore public policy's role in influencing oligopolistic and monopolistic behaviors.

Understand the concept of price discrimination and how tying can be an example of this.

Recognize the effects of resale price maintenance on market competition and its legitimate economic purposes.

Comprehend the implications of the prisoners' dilemma in repeated games and the role of strategies like tit-for-tat.

---

Definitions:

Nativist Approach

A psychological theory proposing that specific abilities or talents are innate or biologically pre-programmed from birth.

Language Acquisition

The process by which humans acquire the ability to perceive, comprehend, and produce language through both innate mechanisms and learned elements.

Innate Capacity

A natural ability or talent that an individual is born with, not acquired through learning.

Relativist

A philosophical stance asserting that points of view have no absolute truth or validity, having only relative, subjective value according to differences in perception and consideration.