Solved

Of the 23 First Year Male Students at State U $\quad$

question 38

Essay

Of the 23 first year male students at State U. admitted from Jim Thorpe High School, 8 were offered baseball scholarships and 7 were offered football scholarships. The University admissions committee looked at the students' composite ACT scores (shown in table), wondering if the University was lowering their standards for athletes. Assuming that this group of students is representative of all admitted students, what do you think?
$\quad$ $\quad$ $\text {Composite ACT Score }$
$\begin{array}{|c|c|c|}\hline\text { Baseball }&\text { Non-athletes }& \text {Football }\\\hline 25 & 21 & 22 \\22 & 27 & 21 \\19 & 29 & 24 \\25 & 26 & 27 \\24 & 30 & 19 \\25 & 27 & 23 \\24 & 26 & 17 \\23 & 23 & \\\hline\end{array}$

Boxplots:

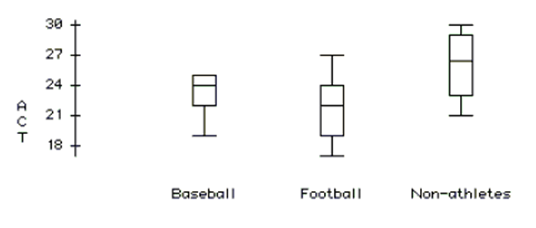
$Of the 23 first year male students at State U. admitted from Jim Thorpe High School, 8 were offered baseball scholarships and 7 were offered football scholarships. The University admissions committee looked at the students' composite ACT scores (shown in table), wondering if the University was lowering their standards for athletes. Assuming that this group of students is representative of all admitted students, what do you think? \quad \quad \text {Composite ACT Score } \begin{array}{|c|c|c|} \hline\text { Baseball }&\text { Non-athletes }& \text {Football }\\ \hline 25 & 21 & 22 \\ 22 & 27 & 21 \\ 19 & 29 & 24 \\ 25 & 26 & 27 \\ 24 & 30 & 19 \\ 25 & 27 & 23 \\ 24 & 26 & 17 \\ 23 & 23 & \\ \hline \end{array} Boxplots: \text {Analysis of Variance Table} \begin{array}{|c|c|r|c|c|c|} \hline &\text { Sums of }&&\text { Mean }&&\text { P-} \\ \text { Source}&\text { Squares } &d f &\text { Squares } &\text { F-ratio }&\text { value }\\ \hline Team & 71.00 & 2 & 35.50 & 4.56 & 0.023 \\ \hline Error & 155.61 & 20 & 7.78 & & \\ \hline Total & 226.61 & 22 & & & \\ \hline \end{array} \text {Means and Std Deviations} \begin{array}{|l|r|r|r|} \hline \text {Level }& \text {Number} & \text {Mean }& \text {Std Dev} \\ \hline \text {Baseball} & 8 & 23.3750 & 2.06588 \\ \hline \text {Football }& 7 & 21.8571 & 3.28778 \\ \hline \text {Non Athlete} & 8 & 26.1250 & 2.94897 \\ \hline \end{array} Normal Probability Plot: -Are the two sports teams mean ACT scores different?$

$\text {Analysis of Variance Table}$
$\begin{array}{|c|c|r|c|c|c|}\hline &\text { Sums of }&&\text { Mean }&&\text { P-} \\ \text { Source}&\text { Squares } &d f &\text { Squares } &\text { F-ratio }&\text { value }\\\hline Team & 71.00 & 2 & 35.50 & 4.56 & 0.023 \\\hline Error & 155.61 & 20 & 7.78 & & \\\hline Total & 226.61 & 22 & & & \\\hline\end{array}$

$\text {Means and Std Deviations}$
$\begin{array}{|l|r|r|r|}\hline \text {Level }& \text {Number} & \text {Mean }& \text {Std Dev} \\\hline \text {Baseball} & 8 & 23.3750 & 2.06588 \\\hline \text {Football }& 7 & 21.8571 & 3.28778 \\\hline \text {Non Athlete} & 8 & 26.1250 & 2.94897 \\\hline\end{array}$

Normal Probability Plot:

$Of the 23 first year male students at State U. admitted from Jim Thorpe High School, 8 were offered baseball scholarships and 7 were offered football scholarships. The University admissions committee looked at the students' composite ACT scores (shown in table), wondering if the University was lowering their standards for athletes. Assuming that this group of students is representative of all admitted students, what do you think? \quad \quad \text {Composite ACT Score } \begin{array}{|c|c|c|} \hline\text { Baseball }&\text { Non-athletes }& \text {Football }\\ \hline 25 & 21 & 22 \\ 22 & 27 & 21 \\ 19 & 29 & 24 \\ 25 & 26 & 27 \\ 24 & 30 & 19 \\ 25 & 27 & 23 \\ 24 & 26 & 17 \\ 23 & 23 & \\ \hline \end{array} Boxplots: \text {Analysis of Variance Table} \begin{array}{|c|c|r|c|c|c|} \hline &\text { Sums of }&&\text { Mean }&&\text { P-} \\ \text { Source}&\text { Squares } &d f &\text { Squares } &\text { F-ratio }&\text { value }\\ \hline Team & 71.00 & 2 & 35.50 & 4.56 & 0.023 \\ \hline Error & 155.61 & 20 & 7.78 & & \\ \hline Total & 226.61 & 22 & & & \\ \hline \end{array} \text {Means and Std Deviations} \begin{array}{|l|r|r|r|} \hline \text {Level }& \text {Number} & \text {Mean }& \text {Std Dev} \\ \hline \text {Baseball} & 8 & 23.3750 & 2.06588 \\ \hline \text {Football }& 7 & 21.8571 & 3.28778 \\ \hline \text {Non Athlete} & 8 & 26.1250 & 2.94897 \\ \hline \end{array} Normal Probability Plot: -Are the two sports teams mean ACT scores different?$

-Are the two sports teams mean ACT scores different?

Definitions:

True Average Age

The actual mean age of a group or population, accurately representing the central tendency without bias.

Sample Size

The number of observations or units in a sample taken from a population for the purpose of statistical analysis.

Critical Value

A threshold value that is compared with the test statistic to determine whether the null hypothesis should be rejected in hypothesis testing.

True Average Weight

The actual mean weight calculated across a specified population or sample.

Of the 23 First Year Male Students at State U \quad

Definitions:

Of the 23 First Year Male Students at State U $\quad$