The Bigger the Stop Sign, the More Expensive It Is $\mathrm{R}$

question 82

Essay

The bigger the stop sign, the more expensive it is. Here is a graph of the height of a sign in inches versus its cost in dollars.

To achieve linearity, the data was transformed using a square root function of cost. Here are the results and a residual plot.
Dependent Variable: sqrt(cost)
$\mathrm{R}$ (correlation coefficient) $=0.98946627$
$R-s q=0.97904349$
s: 0.2141

$\begin{array}{lrr}\text { Parameter } & \text { coeff } & \text { se } \\\text { Intercept } & 1.1857 & 0.4346 \\\text { height } & 0.1792 & 0.0151\end{array}$



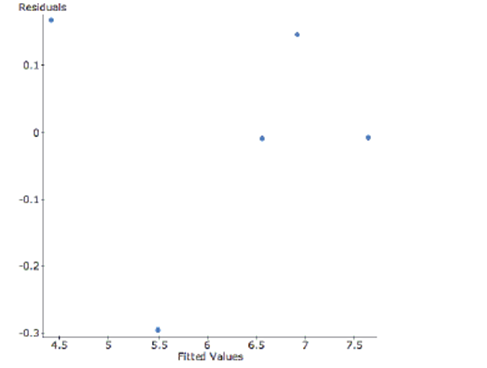
-Do you think this transformation for linearity was successful? Why?

Understand the concept of warranted arguments and when an argument is considered worthy of acceptance.

Comprehend the progression from coincidence to correlation to causal explanations.

Recognize the impact of statistical analysis in evaluating arguments and making generalizations.

Identify the misuse of numbers in arguments and the importance of using appropriate descriptive measures.

---

Definitions:

Payoff-Matrix

A table that shows the potential outcomes or payoffs of different strategies for two or more players in a game.

Game-Tree

A graphical representation of the possible moves in a game, showing the sequential nature of players' actions and choices.

Allocative Efficiency

A state of the economy where resources are distributed in a way that maximizes the net benefit to society, meaning that goods and services are produced and consumed at quantities where the marginal benefit equals marginal cost.

Oligopoly

A market structure characterized by a small number of firms that dominate the market, leading to limited competition and potentially higher prices for consumers.