A Statistics Professor Investigated Some of the Factors That Affect $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$

question 102

Essay

A statistics professor investigated some of the factors that affect an individual student's final grade in his or her course. He proposed the multiple regression model: $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ .
Where:
y = final mark (out of 100). $x _ { 1 }$ = number of lectures skipped. $x _ { 2 }$ = number of late assignments. $X _ { 3 }$ = mid-term test mark (out of 100).
The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS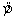
$= 41.6 - 3.18 x _ { 1 } - 1.17 x _ { 2 } + .63 x _ { 3 }$
$\begin{array}{|c|ccc|}\hline \text { Predictor } & \text { Coef } & \text { StDev } & \mathrm{T} \\\hline \text { Constant } & 41.6 & 17.8 & 2.337 \\x_{1} & -3.18 & 1.66 & -1.916 \\x_{2} & -1.17 & 1.13 & -1.035 \\x_{3} & 0.63 & 0.13 & 4.846 \\\hline\end{array}$


$\mathrm{S}=13.74 \quad \mathrm{R}-\mathrm{Sq}=30.0 \%$

ANALYSIS OF VARIANCE
$\begin{array}{|l|cccc|}\hline \text { Source of Variation } & \mathrm{df} & \mathrm{SS} & \mathrm{MS} & \mathrm{F} \\\hline \text { Regression } & 3 & 3716 & 1238.667 & 6.558 \\\text { Error } & 46 & 8688 & 188.870 & \\\hline \text { Total } & 49 & 12404 & & \\\hline\end{array}$ Do these data provide enough evidence to conclude at the 5% significance level that the final mark and the number of skipped lectures are linearly related?

---

Definitions:

Mode

The value that occurs most frequently in a given set of data.

Distribution

In statistics, a mathematical representation of the observed or possible frequencies of occurrences of a range of outcomes.

Normally Distributed

A statistical term describing data that fall into a symmetrical, bell-shaped curve where most observations cluster around the mean.

Standard Deviation

An analytical tool that assesses the level of diversity or deviation of data points from their central value.