SCENARIO 14-8
A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X1 = Age) and experience in the field (X2 = Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output:
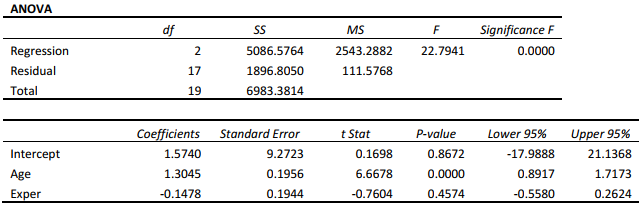
Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8,the value of the F-statistic for testing the significance of the entire regression is .
Definitions:
Margin of Error
An expression of the amount of random sampling error in a survey's results, indicating a range within which the true population parameter is likely to lie.
Confidence Interval
A collection of values, derived from the analysis of sample data, that is expected to cover the value of an unknown population quality.
Standard Error
A measure of the accuracy with which a sample distribution represents a population by using the standard deviation of the sample.
Confidence Interval
A set of numbers, taken from sample-based statistics, that is probable to contain the estimated value of an unspecified population parameter.
Q17: Each forecast using the method of exponential
Q65: Referring to Scenario 15-6,what is the value
Q82: In multidimensional scaling,the stress statistic is used
Q82: Referring to Scenario 14-15,the null hypothesis<br>H<sub>0</sub>:
Q90: In k-means clustering,observations that are assigned to
Q122: Referring to Scenario 12-3,the expected cell frequency
Q129: Referring to Scenario 12-5,there is sufficient evidence
Q158: Referring to Scenario 14-15,the null hypothesis<br>H<sub>0</sub>:
Q165: Referring to Scenario 12-7,what are the values
Q226: Referring to Scenario 14-3,the p-value for the