Find the Critical Point(s) of the Function

question 143

Multiple Choice

Find the critical point(s) of the function.Then use the second derivative test to classify the nature of each point, if possible.Finally, determine the relative extrema of the function.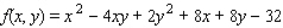

• A)(8, - 6); relative minimum value: f(8, - 6) = - 24
• B)(- 8, 6); relative maximum value: f(- 8, 6) = - 56
• C)(8, 6); saddle point: f(8, 6) = 24
• D)there are no critical points

---

Definitions:

Mining Safety

Practices, procedures, and regulations designed to minimize health and safety risks to workers in the mining industry.

Modeling Process

The psychological mechanism through which individuals learn new behaviors or attitudes by observing others.

Bandura

Albert Bandura was a distinguished psychologist, renowned for his contributions to the social learning theory and the notion of self-efficacy.

Observational Learning

Observational learning is the process of acquiring new behaviors or knowledge by watching and imitating others, a key concept of social learning theory.