A Statistics Professor Investigated Some of the Factors That Affect $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$

question 69

Essay

A statistics professor investigated some of the factors that affect an individual student's final grade in his or her course. He proposed the multiple regression model: $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ .
Where:
y = final mark (out of 100). $x _ { 1 }$ = number of lectures skipped. $x _ { 2 }$ = number of late assignments. $x _ { 3 }$ = mid-term test mark (out of 100).
The professor recorded the data for 50 randomly selected students. The computer output is shown below.
THE REGRESSION EQUATION IS 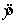= $41.6 - 3.18 x _ { 1 } - 1.17 x _ { 2 } + .63 x _ { 3 }$ $$\begin{array} { | c | c c c | } \hline \text { Predictor } & \text { Coef } & \text { StDev } & \mathrm { T } \\\hline \text { Constant } & 41.6 & 17.8 & 2.337 \\x _ { 1 } & - 3.18 & 1.66 & - 1.916 \\x _ { 2 } & - 1.17 & 1.13 & - 1.035 \\x _ { 3 } & 0.63 & 0.13 & 4.846 \\\hline\end{array}$$ S = 13.74 R-Sq = 30.0%. $$\begin{array}{l}\text { ANALYSIS OF VARIANCE }\\\begin{array} { | l | c c c c | } \hline \text { Source of Variation } & \mathrm { df } & \text { SS } & \text { MS } & \text { F } \\\hline \text { Regression } & 3 & 3716 & 1238.667 & 6.558 \\\text { Error } & 46 & 8688 & 188.870 & \\\hline \text { Total } & 49 & 12404 & & \\\hline\end{array}\end{array}$$ Do these data provide enough evidence to conclude at the 5% significance level that the model is useful in predicting the final mark?

---

Definitions:

Coppertone

A brand famous for its sun protection products, such as sunscreens and lotions, designed to shield the skin from harmful UV rays.

SPF Level

A measure of the protection a sunscreen product offers against the sun's ultraviolet (UV) rays, indicating how long a person can be exposed to the sun without getting sunburned.

Selective Perception

The psychological process by which individuals perceive what they want to in media messages while ignoring opposing viewpoints.

Selective Exposure

The tendency of individuals to prefer information that supports their pre-existing beliefs and values, avoiding contradictory evidence.