Mountainside State Park Has Four Visitor Centers

question 19

Essay

Mountainside State Park has four visitor centers. To study the operation of these centers, a DEA model has been developed that compares inputs (size, number of staff, weekly hours of operation) and outputs (% of visitors attending educational program, daily sales in gift shop). The computer solution is shown below. What can you conclude about the efficiency of the North center?
LINEAR PROGRAMMING PROBLEM
Min
1E+0wn+0ws+0we+0ww
s.t.
1) −400E+400wn+1200ws+2400we+1500ww<0
2) −3E+3wn+6ws+10we+7ww<0
3) −56E+56wn+108ws+92we+108ww<0
4) −49E+49wn+83ws+56we+72ww>0
5) −38E+38wn+425ws+1200we+630ww>0
6) +1wn+1ws+1we+1ww=1
​
OPTIMAL SOLUTION
Objective Function Value = 1.000 ​

---

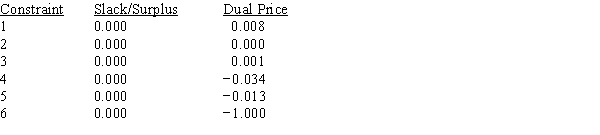
Definitions:

Producer Surplus

The difference between what producers are willing to accept for a good or service and the actual price they receive, representing economic gain.

Marginal Cost

The increase in total cost that arises from producing one additional unit of a product or service.

Maximize Profit

To maximize profit, a firm seeks to increase the difference between its total revenues and total costs through optimal pricing strategies and efficient production.

Marginal Cost

Marginal cost represents the increase or decrease in the total cost of production when the quantity produced is incremented by one unit.