The Linear Programming Problem

question 18

Essay

The linear programming problem:
Max
6x₁ + 2x₂ + 3x₃ + 4x₄
s.t.
x₁ + x₂ + x₃ + x₄ ≤ 100
4x₁ + x₂ + x₃ + x₄ ≤ 160
3x₁ + x₂ + 2x₃ + 3x₄ ≤ 240
x₁, x₂, x ₃, x₄ ≥ 0
​
has the final tableau: ​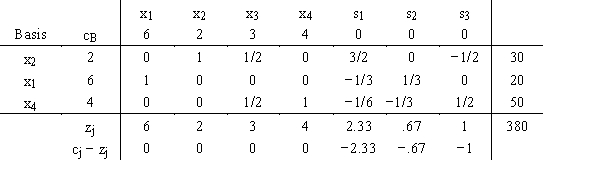
Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem.
LINEAR PROGRAMMING PROBLEM
MAX
6X1+2X2+3X3+4X4
S.T.
1) 1X1 + 1X2 + 1X3 + 1X4 < 100
2) 4X1 + 1X2 + 1X3 + 1X4 < 160
3) 3X1 + 1X2 + 2X3 + 3X4 < 240
​
OPTIMAL SOLUTION
Objective Function Value = ​ ​
OBJECTIVE COEFFICIENT RANGES ​
RIGHT HAND SIDE RANGES

---

Definitions:

Variable Cost

Costs that vary in direct relation to a business's operations, like expenses for raw materials or manufacturing supplies.

Activity Decreases

Reductions in the volume or intensity of activities, often leading to lower costs or changes in operational strategies.

Cost Estimation

The process of predicting the amount of resources, especially money, time, and labor, necessary to complete a project or produce a product.

Strong Correlation

A statistical relationship between two variables where a change in one is strongly associated with a change in the other.