The Linear Programming Problem

question 18

Essay

The linear programming problem:
Max
6x₁ + 2x₂ + 3x₃ + 4x₄
s.t.
x₁ + x₂ + x₃ + x₄ ≤ 100
4x₁ + x₂ + x₃ + x₄ ≤ 160
3x₁ + x₂ + 2x₃ + 3x₄ ≤ 240
x₁, x₂, x ₃, x₄ ≥ 0
​
has the final tableau: ​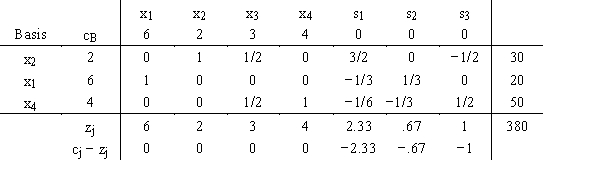
Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem.
LINEAR PROGRAMMING PROBLEM
MAX
6X1+2X2+3X3+4X4
S.T.
1) 1X1 + 1X2 + 1X3 + 1X4 < 100
2) 4X1 + 1X2 + 1X3 + 1X4 < 160
3) 3X1 + 1X2 + 2X3 + 3X4 < 240
​
OPTIMAL SOLUTION
Objective Function Value = ​ ​
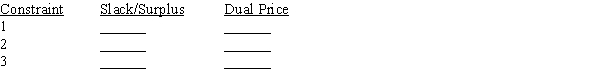
OBJECTIVE COEFFICIENT RANGES ​
RIGHT HAND SIDE RANGES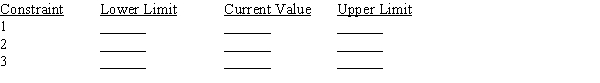

---

Definitions:

Cocaine

A powerful stimulant drug derived from the leaves of the coca plant, which can cause intense euphoria but also significant physical and psychological harm.

Coca Plant

A plant native to South America, known scientifically as Erythroxylum coca, from which cocaine is derived.

Activation-Synthesis Theory

A theory of dreaming that proposes dreams are the result of the brain's attempt to make sense of neural activity that occurs during sleep.

Brainstem Signals

Neural transmissions within the brainstem, which is responsible for basic life functions such as breathing, heart rate, and blood pressure.