Cesium 137 (Cs¹³⁷)is a Short-Lived Radioactive Isotope $e^{-\left(\frac{\ln 2}{30}\right) t}$

question 127

Short Answer

Cesium 137 (Cs¹³⁷)is a short-lived radioactive isotope.It decays at a rate proportional to the amount of itself present and has a half-life of 30 years (i.e., the amount of Cs¹³⁷ remaining t years after A₀ mg of the radioactive isotope is released is given by 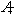$e^{-\left(\frac{\ln 2}{30}\right) t}$ ).As a result of its operations, a nuclear power plant releases Cs¹³⁷ at a rate of 0.14 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Since Cs¹³⁷ poses a great health risk, the government says that the maximum amount of Cs¹³⁷ acceptable in the surrounding environment is 1 mg (spread over the surroundings).How many mg per year of the isotope can the station release and still be in compliance with the regulations? Round to 2 decimal places.