SCENARIO 12-12
the Manager of the Purchasing Department of a Large

question 85

True/False

SCENARIO 12-12
The manager of the purchasing department of a large saving and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan
application.Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded.Below is the regression output: $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.9447 \\\text { R Square } & 0.8924 \\\text { Adjusted R } & 0.8886 \\\text { Square } & \\\text { Standard } & 0.3342 \\\text { Error } & \\\text { Observations } & 30 \\\hline\end{array}\\\text { ANOVA }\\\begin{array} { l r r r r r } \hline & { \text { df } } & { \text { SS } } & { \text { MS } } & \text { F } & \text { Significance } F \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & & \\\hline\end{array}\\\begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\text { Applications } & 0.0126 & 0.0008 & 15.2388 & 0.0000 & 0.0109 & 0.0143 \\\text { Recorded } & & & & & & \\\hline\end{array}\end{array}$$ 12-46 Simple Linear Regression 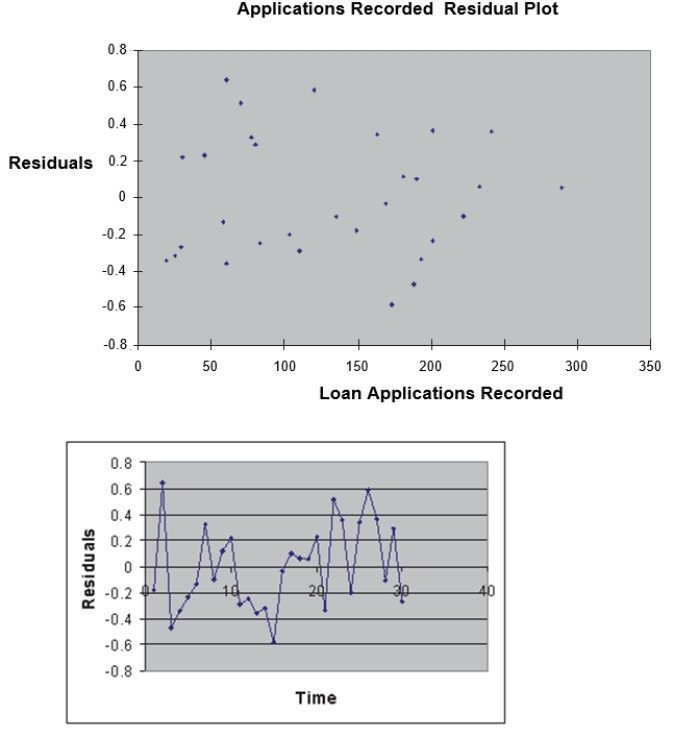Simple Linear Regression 12-47
-Referring to Scenario 12-12, you can be 95% confident that the mean amount of time needed to record one additional loan application is somewhere between 0.0109 and 0.0143 hours.

---

Definitions:

High Absenteeism Rate

A situation where there is a consistently high number of instances where employees are absent from work, often indicating underlying issues.

Focusing On Narrow Areas

The practice of dedicating efforts or resources towards a specific and limited field of work or study to achieve expertise or efficiency.

Externalizing

Projecting one's own feelings, responses, or thoughts onto the external world or other people.

Collaborative Computing

Collaborative computing refers to technologies and practices that enable individuals to work together on shared tasks or projects, typically in a digital environment.