SCENARIO 12-12
the Manager of the Purchasing Department of a Large

question 97

Multiple Choice

SCENARIO 12-12
The manager of the purchasing department of a large saving and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan
application.Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded.Below is the regression output: $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.9447 \\\text { R Square } & 0.8924 \\\text { Adjusted R } & 0.8886 \\\text { Square } & \\\text { Standard } & 0.3342 \\\text { Error } & \\\text { Observations } & 30 \\\hline\end{array}\\\text { ANOVA }\\\begin{array} { l r r r r r } \hline & { \text { df } } & { \text { SS } } & { \text { MS } } & \text { F } & \text { Significance } F \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & & \\\hline\end{array}\\\begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\text { Applications } & 0.0126 & 0.0008 & 15.2388 & 0.0000 & 0.0109 & 0.0143 \\\text { Recorded } & & & & & & \\\hline\end{array}\end{array}$$ 12-46 Simple Linear Regression 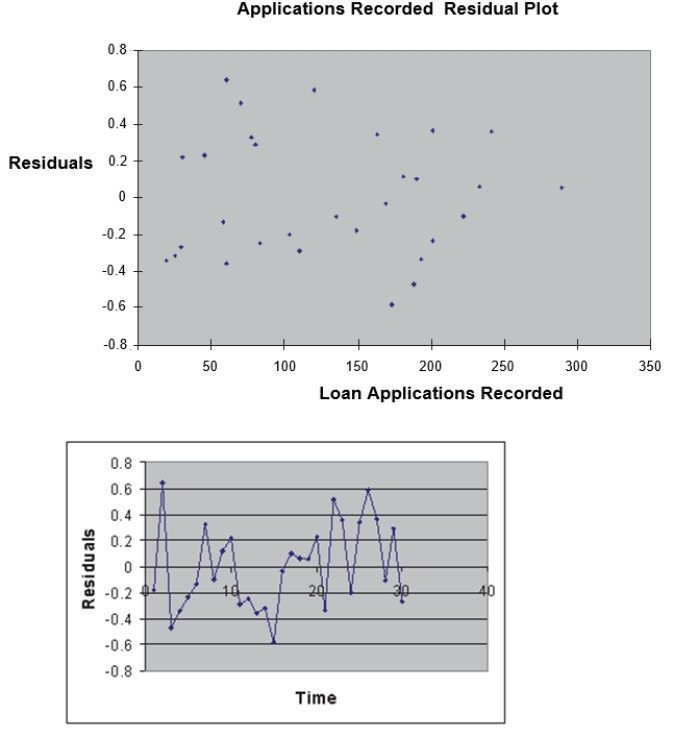Simple Linear Regression 12-47
-Referring to Scenario 12-12, the value of the measured t-test statistic to test whether the amount of time depends linearly on the number of loan applications recorded is

• A)0.8924
• B)3.2559
• C)15.2388
• D)232.2200

---

Definitions:

Population Proportion

The ratio of a specific subgroup within a population to the entire population, typically expressed as a percentage.

Independent Random Samples

Samples selected from a population in such a way that each member has an equal chance of being chosen, with no dependence between the selections.

Standard Error

The standard deviation of the sampling distribution of a statistic, commonly used to estimate the accuracy of sample mean as a predictor of the population mean.

Pooled Estimate

Combining estimates from different populations to obtain a single estimate that is more accurate and has a higher power due to a larger sample size.