Solved

SCENARIO 12-11
a Computer Software Developer Would Like to Use

question 122

Multiple Choice

SCENARIO 12-11
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression
along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$SCENARIO 12-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|r|r|r|r|r|} \hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & \\ \hline \end{array} Simple Linear Regression 12-41 -Referring to Scenario 12-11, which of the following is the correct interpretation for the slope coefficient? A) For each decrease of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. B) For each increase of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. C) For each decrease of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands. D) For each increase of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands.$ $\begin{array}{lr}{\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000 \\\hline\end{array}$

$\text { ANOVA }$
$\begin{array}{|l|r|r|r|r|r|}\hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & \\\hline\end{array}$

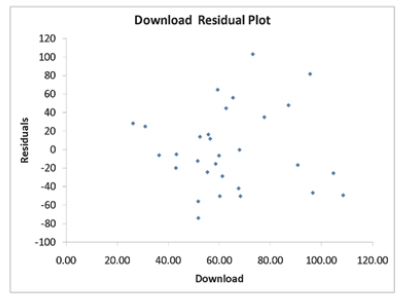$SCENARIO 12-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|r|r|r|r|r|} \hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & \\ \hline \end{array} Simple Linear Regression 12-41 -Referring to Scenario 12-11, which of the following is the correct interpretation for the slope coefficient? A) For each decrease of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. B) For each increase of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. C) For each decrease of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands. D) For each increase of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands.$

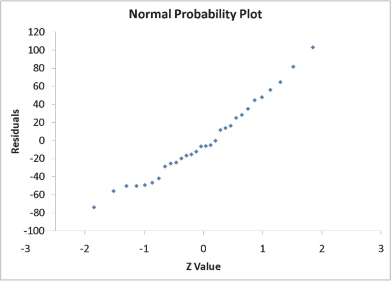
$SCENARIO 12-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|r|r|r|r|r|} \hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & \\ \hline \end{array} Simple Linear Regression 12-41 -Referring to Scenario 12-11, which of the following is the correct interpretation for the slope coefficient? A) For each decrease of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. B) For each increase of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. C) For each decrease of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands. D) For each increase of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands.$ Simple Linear Regression 12-41 $SCENARIO 12-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} \text { ANOVA } \begin{array}{|l|r|r|r|r|r|} \hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & \\ \hline \end{array} Simple Linear Regression 12-41 -Referring to Scenario 12-11, which of the following is the correct interpretation for the slope coefficient? A) For each decrease of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. B) For each increase of 1 thousand downloads, the expected revenue is estimated to increase by $ 3.7297 thousands. C) For each decrease of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands. D) For each increase of 1 thousand dollars in expected revenue, the expected number of downloads is estimated to increase by 3.7297 thousands.$
-Referring to Scenario 12-11, which of the following is the correct interpretation for the slope coefficient?

Discuss the requirements set by insurance contracts for insured parties to maintain safety and security standards.

Understand the concept of externalities and their impact on social welfare.

Analyze how government interventions, such as taxes and subsidies, can address externalities.

Comprehend the role of property rights in resolving disputes over external costs and benefits.

Definitions:

Inventory Turnover

A proportion indicating the frequency with which a business has sold its inventory and replenished it within a specific timeframe.

Current Liabilities

Financial obligations of a business that are due and payable within one year, including accounts payable, short-term debt, and other short-term obligations.

Quick Ratio

The quick ratio, or acid-test ratio, measures a company's ability to meet its short-term obligations with its most liquid assets.

Current Ratio

A financial metric used to evaluate a company's ability to pay short-term obligations, calculated by dividing current assets by current liabilities.

SCENARIO 12-11 a Computer Software Developer Would Like to Use

Definitions:

SCENARIO 12-11
a Computer Software Developer Would Like to Use