SCENARIO 12-11
a Computer Software Developer Would Like to Use

question 63

Short Answer

SCENARIO 12-11
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression
along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}{\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000 \\\hline\end{array}$

$\text { ANOVA }$
$\begin{array}{|l|r|r|r|r|r|}\hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & \\\hline\end{array}$





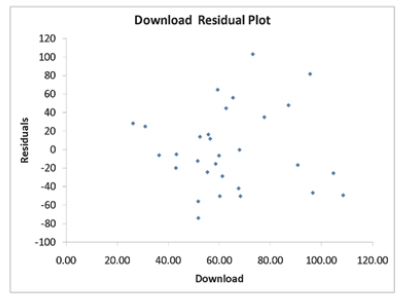Simple Linear Regression 12-41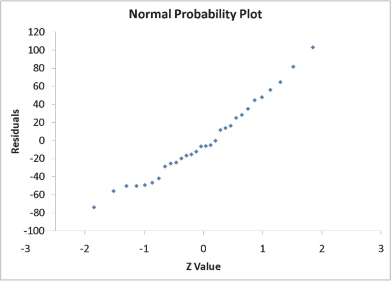
-Referring to Scenario 12-11, what do the lower and upper limits of the 95% confidence interval estimate for population slope?

---

Definitions:

Ethicality

Pertaining to or dealing with morals or the principles of morality; pertaining to right and wrong in conduct.

Confidential Information

Sensitive information that is not to be shared with unauthorized persons, often protected due to its private or proprietary nature.

Cellphone Screen

The display area of a mobile phone where information, icons, and media are visually presented to the user.

Data Security

The practices, policies, and technologies used to protect digital information from unauthorized access, corruption, or theft.