SCENARIO 12-12
the Manager of the Purchasing Department of a Large

question 158

True/False

SCENARIO 12-12
The manager of the purchasing department of a large saving and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan
application.Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded.Below is the regression output: $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.9447 \\\text { R Square } & 0.8924 \\\text { Adjusted R } & 0.8886 \\\text { Square } & \\\text { Standard } & 0.3342 \\\text { Error } & \\\text { Observations } & 30 \\\hline\end{array}\\\text { ANOVA }\\\begin{array} { l r r r r r } \hline & { \text { df } } & { \text { SS } } & { \text { MS } } & \text { F } & \text { Significance } F \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & & \\\hline\end{array}\\\begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\text { Applications } & 0.0126 & 0.0008 & 15.2388 & 0.0000 & 0.0109 & 0.0143 \\\text { Recorded } & & & & & & \\\hline\end{array}\end{array}$$ 12-46 Simple Linear Regression 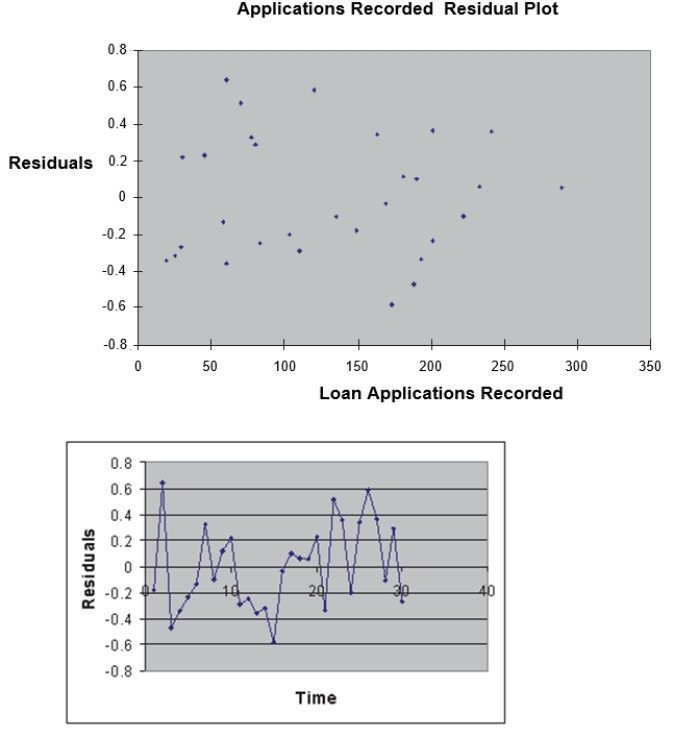Simple Linear Regression 12-47
-Referring to Scenario 12-12, there is sufficient evidence that the amount of time needed linearly depends on the number of loan applications at a 1% level of significance.

---

Definitions:

Relationship Dependence

The extent to which the outcomes of a project or business endeavor depend on the strength and nature of relationships between stakeholders.

Complex Systems

Systems characterized by multiple interacting components whose behavior cannot be easily predicted due to the interactions at different scales and feedback loops.

Adaptability

The capability to adjust to new conditions or changes in the environment or circumstances efficiently.

Nonlinear Systems

Systems in which the output is not directly proportional to the input, often characterized by complex, unpredictable behavior.