SCENARIO 12-12
the Manager of the Purchasing Department of a Large

question 90

Short Answer

SCENARIO 12-12
The manager of the purchasing department of a large saving and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan
application.Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded.Below is the regression output: $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.9447 \\\text { R Square } & 0.8924 \\\text { Adjusted R } & 0.8886 \\\text { Square } & \\\text { Standard } & 0.3342 \\\text { Error } & \\\text { Observations } & 30 \\\hline\end{array}\\\text { ANOVA }\\\begin{array} { l r r r r r } \hline & { \text { df } } & { \text { SS } } & { \text { MS } } & \text { F } & \text { Significance } F \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & & \\\hline\end{array}\\\begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\text { Applications } & 0.0126 & 0.0008 & 15.2388 & 0.0000 & 0.0109 & 0.0143 \\\text { Recorded } & & & & & & \\\hline\end{array}\end{array}$$ 12-46 Simple Linear Regression 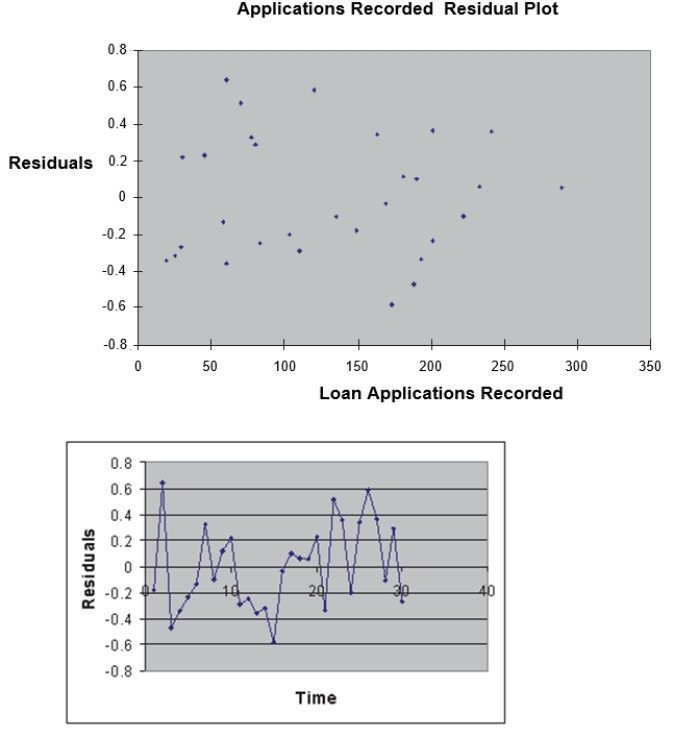Simple Linear Regression 12-47
-Referring to Scenario 12-12, to test the claim that the mean amount of time depends positively on the number of loan applications recorded against the null hypothesis that the mean amount of time does not depend linearly on the number of invoices processed, the p-value of the test statistic is .

---

Definitions:

Undiscounted Sum

The total of all future cash flows associated with an investment or project without adjusting them for their present value.

Discounted

The method of calculating the current value of a future sum of money or series of cash flows using a particular return rate.

Interest Expense

The financial charges a company bears for loaned money across a time frame.

Note Payable-National Bank

A written promise to pay a specific sum of money, borrowed from a national bank, at a future date.