Consider the following two games:
Game 1: There are 10 balls of different colors, you pick one of the proposed balls. After you have made your choice and have put the ball back, one ball is selected at random. If the selected ball matches the ball you picked, you win.
Game 2: There are 6 balls of different colors, you pick two of the proposed balls. After you have made your choices and have put balls back, two different balls are selected at random. If the selected balls match the two you picked, you win.
If you can only play one of these games, which game would you pick to win and why? Use relevant probabilities to justify your choice.
A)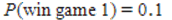 and
and  , therefore it is advantageous to play game 1 because the probability of winning is higher.
, therefore it is advantageous to play game 1 because the probability of winning is higher.
B)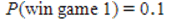 and
and  , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
C)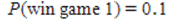 and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
D)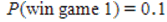 and
and 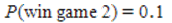 , therefore it is no matter what game to play because the probabilities of winning are equal.
, therefore it is no matter what game to play because the probabilities of winning are equal.
E)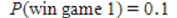 and
and  , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
Definitions:
Current Asset Account
An account on the balance sheet representing the value of assets that are expected to be converted into cash, sold, or consumed within a year or the operating cycle, whichever is longer.
Inventory Returns Estimated
An accounting estimate of the goods that will be returned by customers and subtracted from sales revenue.
Period-End Adjusting Entry
Journal entries made at the end of an accounting period to update the balances of certain accounts and ensure compliance with the accrual basis of accounting.
Revenue Recognition Rules
Accounting principles that determine when and how revenue is recognized in the financial statements.
Q2: Assuming a random sample from a large
Q3: When planning for the big Statistics Department
Q3: Data from a poll of adults aged
Q10: How are the quantities, p and <img
Q13: An article describes an experiment that investigated
Q17: In many areas of the U.S., honey
Q20: We have distinguished two types of studies:
Q31: The % by weight of the element
Q32: The dot plot below shows the annual
Q66: Corporate strategy determines the means for utilizing