Write the Word or Phrase That Best Completes Each Statement $$\left\{ \begin{array} { l } \frac { 1 } { x } + \frac { 1 } { y } = 13 \\\frac { 1 } { x } - \frac { 1 } { y } = 1\end{array} \right.$$

question 29

Multiple Choice

Write the word or phrase that best completes each statement or answers the question.
The revenue equation for a certain brand of mouthwash is y = 1.3x, where x is the number of bottles of mouthwash sold
and y is the total income for selling x bottles. The cost equation is y = 0.5x + 2500, where x is the number of bottles of
mouthwash manufactured and y is the cost of producing x bottles. The following set of axes shows the graph of the cost
and revenue equations.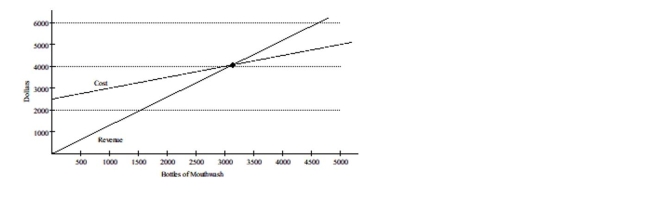
- $$\left\{ \begin{array} { l } \frac { 1 } { x } + \frac { 1 } { y } = 13 \\\frac { 1 } { x } - \frac { 1 } { y } = 1\end{array} \right.$$

• A) \(\left( \frac { 1 } { 6 } , \frac { 1 } { 7 } \right)\)
• B) \(\left( \frac { 1 } { 7 } , \frac { 1 } { 6 } \right)\)
• C) \(\left( \frac { 1 } { 13 } , 0 \right)\)
• D) \(\varnothing\)

---

Definitions:

Output

The total amount of something produced by a person, machine, or industry.

Average Variable Cost

The total variable costs (costs that change with production levels) divided by the quantity of output produced.

Output

The total quantity of goods or services produced within a specific period by a firm or industry.

Diminishing Marginal Returns

A principle stating that as additional units of a variable input are added to a fixed input, the additional output from each new unit of input will eventually decrease.