You Have Read About the So-Called Catch-Up Theory by Economic $X_{1}$

question 55

Essay

You have read about the so-called catch-up theory by economic historians, whereby nations
that are further behind in per capita income grow faster subsequently.If this is true
systematically, then eventually laggards will reach the leader.To put the theory to the test,
you collect data on relative (to the United States)per capita income for two years, 1960 and
1990, for 24 OECD countries.You think of these countries as a population you want to
describe, rather than a sample from which you want to infer behavior of a larger population.
The relevant data for this question is as follows: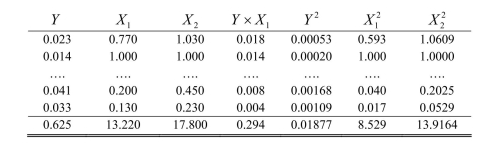
where $X_{1}$ and $X_{2}$ are per capita income relative to the United States in 1960 and 1990 respectively, and $Y$ is the average annual growth rate in $X$ over the $1960-1990$ period. Numbers in the last row represent sums of the columns above.

(a) Calculate the variance and standard deviation of $X_{1}$ and $X_{2}$ . For a catch-up effect to be present, what relationship must the two standard deviations show? Is this the case here?

Understand the function and importance of non-posting accounts in the accounting system.

Identify and describe different types of accounts (assets, liabilities, equity, income, and expense) and their roles in financial statements.

Acquire the ability to navigate QuickBooks, including account creation, sorting, and user access setup.

Differentiate between temporary and permanent accounts and their relevance to financial reporting.

---

Definitions:

Physical Stimulation

Activities or actions that invoke a sensory or physical response, often used in developmental and therapeutic contexts.

Upright

Refers to a position or posture where an individual or object is vertical and straight, typically in contrast to being horizontal or lying down.

Balance

The ability to maintain a stable and controlled body position while stationary or moving.

Motor Activity

Bodily movements produced by skeletal muscles that result in energy expenditure; essential for various physical actions.