Solve the Problem $$p ( x ) = 3 ( x + 3 ) ^ { 3 } - 3$$

question 19

Multiple Choice

Solve the problem.
- $$p ( x ) = 3 ( x + 3 ) ^ { 3 } - 3$$
a. Identify the power function of the form $y = x ^ { n }$ that is the parent function to the given graph.
b. In order, outline the transformations that would be required on the graph of $y = x ^ { n }$ to make the graph of the given function.
c. Match the function with the graph.
i.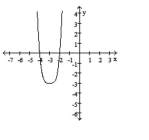


ii.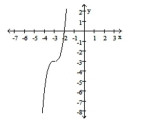

iii.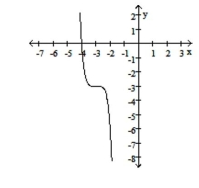


iv.

• A) a. \(y = x ^ { 3 }\) b. Shift \(y = x ^ { 3 }\) to the left 3 units. Stretch vertically by a factor of 3 . Shift downward 3 units. c. Graph iii.
• B) a. \(y = x ^ { 3 }\) b. Shift \(y = x ^ { 3 }\) to the left 3 units. Stretch vertically by a factor of 3 . Shift downward 3 units. c. Graph ii.
• C) a. \(y = x ^ { 3 }\) b. Shift \(y = x ^ { 3 }\) to the left 3 units. Stretch vertically by a factor of 3 . Shift downward 3 units. c. Graph i.
• D) a. \(y = x ^ { 3 }\) b. Shift \(y = x ^ { 3 }\) to the left 3 units. Shrink vertically by a factor of \(\frac { 1 } { 3 }\). Shift downward 3 units. c. Graph iv.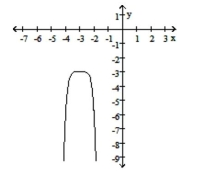

---

Definitions:

Compound Interest

Interest calculated on the initial principal, which also includes all of the accumulated interest of previous periods of a deposit or loan.

Time Periods

Specific durations of time used for accounting purposes, such as fiscal quarters or years.

Discounted

The process of determining the present value of a future amount by applying a discount rate.

Present Value

The current value of a future sum of money or stream of cash flows, discounted at a specified rate of return.